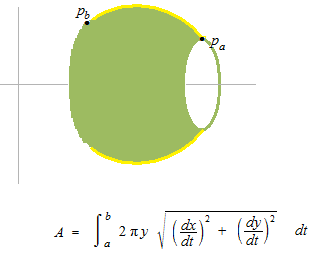Parametric equation
Consider a point P doing a circular motion with radius R. The curve in the x-y plane is a circle. This curve cannot represent the rotation. With t-axis for time, the curve will be shaped in a spiral form like a spring, it will not be a circle. But the length and the surface area will not have right values. The curve in three dimensions on a sheet of paper requires our imagination. If the point P were in a spiral movement in three dimensions, you should have to make a four dimensions curve. As the math always looking for simplicity, an addition of a dimension must be avoided. A curve is a visualization of an equation. We can not draw a curve without equation. Can you represent a circular motion using only equations?
Many natural phenomena are in a rotational movement which is not an exact circle. For this, the expression x-y is not a good choice, because there is no rotational idea.
An equation of a rotation will not be a function.
The rotation repeats over and over.
The time variable t is used.
Polar coordinates locates a point P in the plane using distance and angle, ( r, θ )
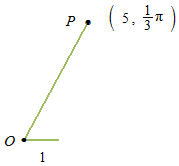
The same point P can be written in rectangular coordinates.
x= rcosθ y = r sin θ
r2 = x2 + y2
Here are two exanples of conversion between an equation in polar coordinates
with r , θ and an equation in rectangular coordinates with x, y .
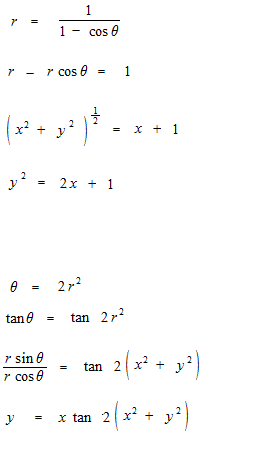
To calculate the area enclosed by a curve of a polar equation, area of circular sector is used.
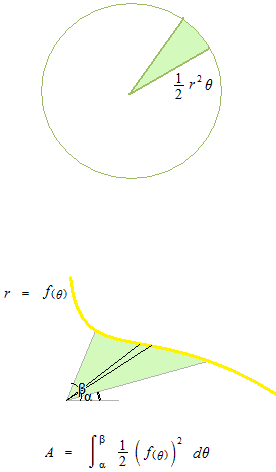
Example of area enclosed by a curve of polar equation. In this example, the equation is not a function; area is calculated separately.
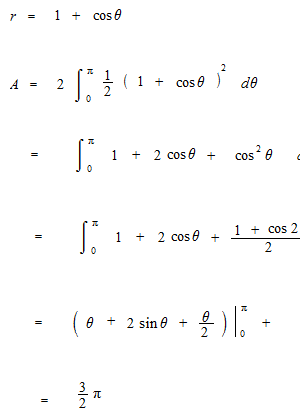
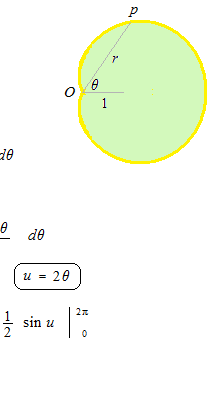
Parametric equation
In this page, t is parameter.
Parametric equation is an expression with a new variable.
First there is a normal equation with two variable. x and y.
A pair of parametric equations express this equation with a new variable.
x will be expressed only with t .
y will be expressed only with t .
The point P which does a cercular movement with radius R.
It turns one round in 2 seconds.
Here’s a pair of parametric equations.
x = R cos πt
y = R sin πt
Cycloid
Parametric equation of a cycloid which turns one round each two seconds.
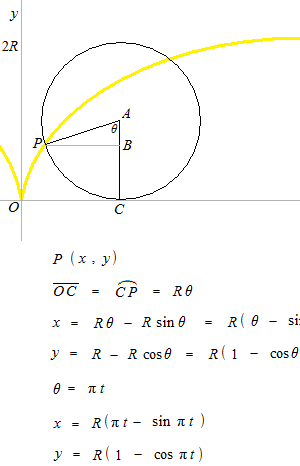
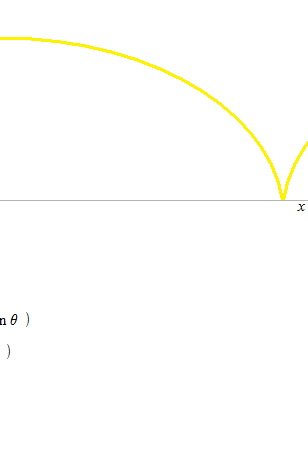
Arc length of a curve of a parametric equation.
Integral of the length of the curve from t = a to t = b.
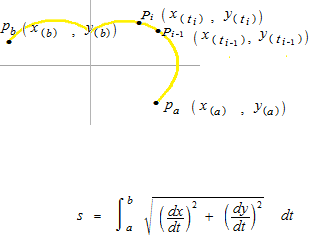
When you are not sure where is dt , you can rather think of dθ. As using arc length, area of solid of revolution can be calculated.