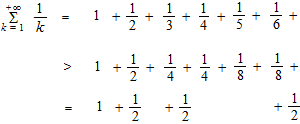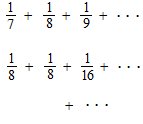Infinite series
As comparing with the curve of this function, we are going to see improper integral, sequence and series. But, first, we start with indefinite integral of this function.
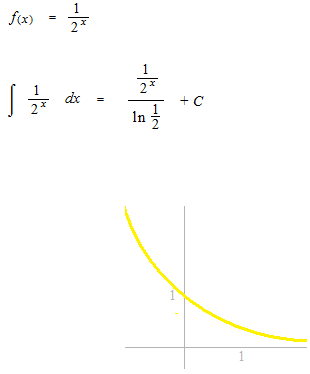
Improper integral.
A kind of definite integral. But one side of interval is not a certain number. When the limite exists, namely when the function is convergent, the value of the limite is an improper integral. We calculate the improper integral from 1 to positive infinity.
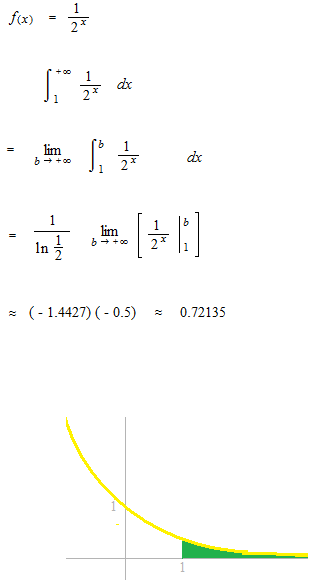
Sequences
A sequence is a function of which the domain is the set of positive integers.
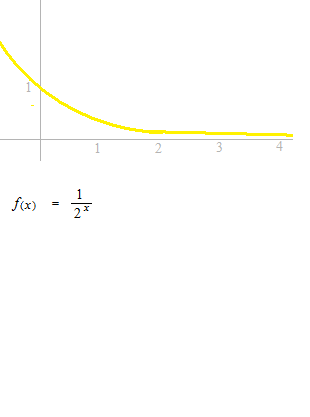
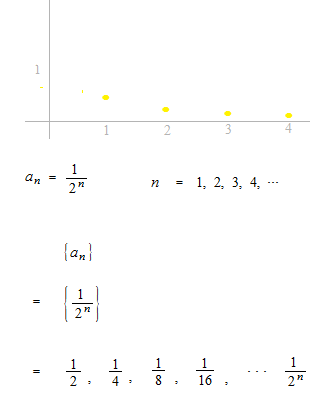
Convergence of sequence
{sn}
| sn ─ L | < ε for all integers n> N
When there is a limit, the sequence is convergent, otherwise divergent.
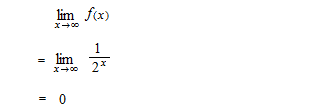
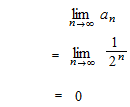
partial sums
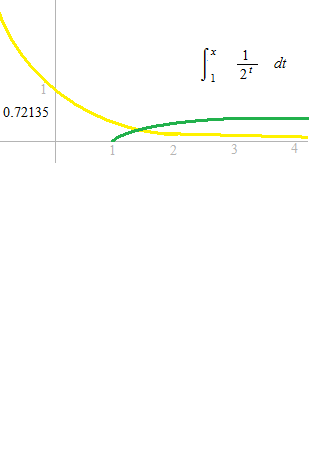
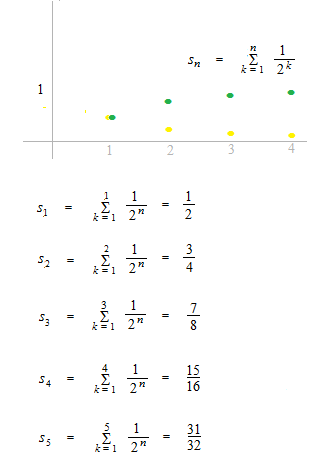
Sequence of partial sums
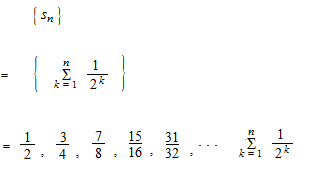
Series
limit of the sequence of partial sums
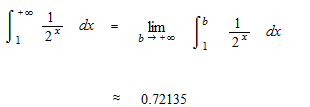
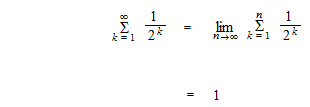
Convergence of sequence is one thing and convergence of series is another.

Telescoping series
Very often, a series calculation is done by an inspiration.
an example
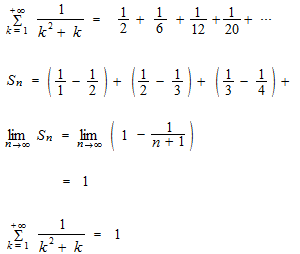
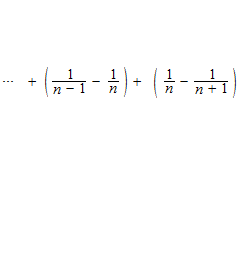
geometric series
A geometric sequence is a sequence of which ratio between every two terms is identical.
A geometric series converges when its ration r is − 1 < r < 1 .
Example
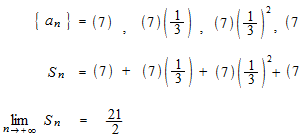
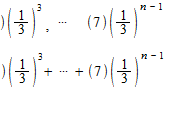
![]()
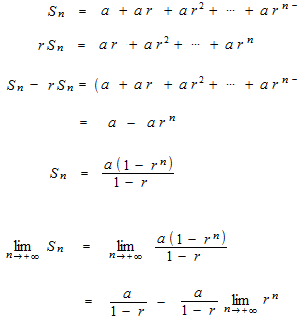
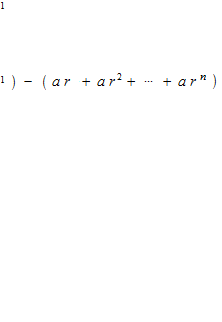
r = 1
Sn= a + a + a + ∙ ∙ ∙ + a = na divergente
r = − 1
Sn= a − a + a − a + ∙ ∙ ∙ + an divergente
Harmonic series
![]()
![]()
Harmonic series diverges.