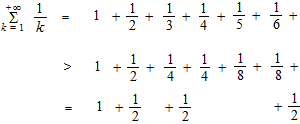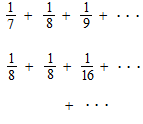Séries infinies
En faisant des comparaisons avec cette fonction, nous allons regarder l’intégrale impropre, la suite et la série.
Commençons par l’intégrale indéfinie de cette fonction.
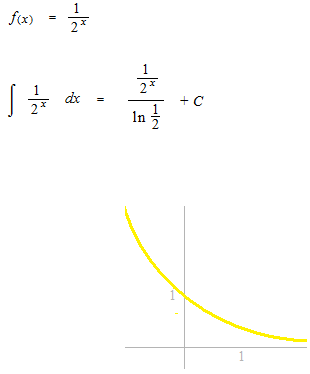
l’intégrale impropre
Une sorte d’intégrale définie avec une borne infinie. S’il a la limite, c’est-à-dire, si cette fonction est convergente, cette limite s’appelle intégrale impropre. Nous allons chercher la limite d’aire à partir de 1.
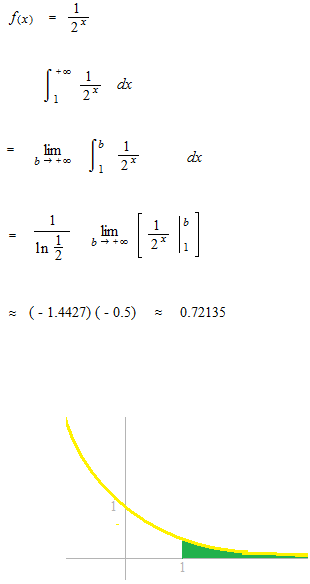
Suite
Quand le domaine de définition de la fonction est l’ensemble des entiers naturels, cette fonction peut s’appeler suite.
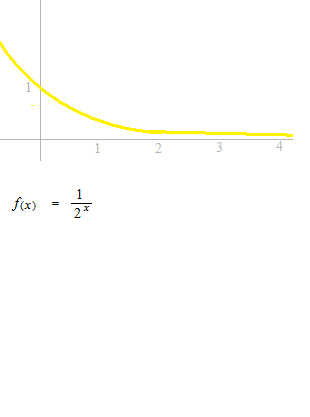
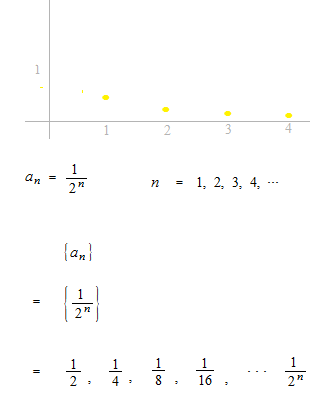
On met souvent les termes entre parentèses. ( a1, a2, a3, a4 )
Convergence de suite
{sn}
| sn ─ L | < ε entier naturel n> N
Quand il y a la limite, la suite est convergente, sinon divergente.
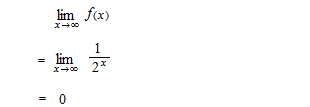
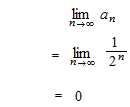
Somme partielle
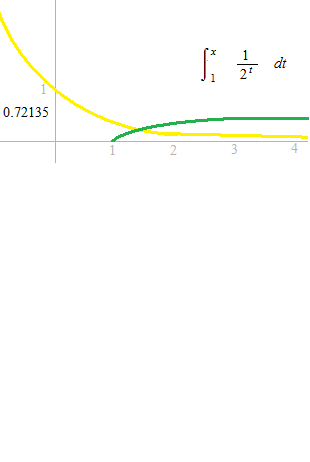
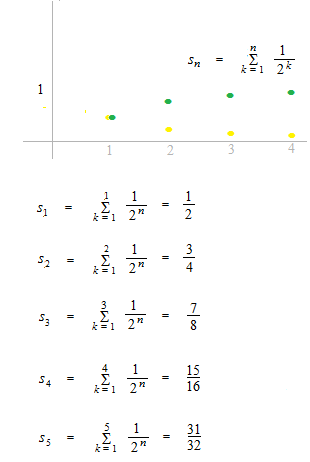
Suite des sommes partielles
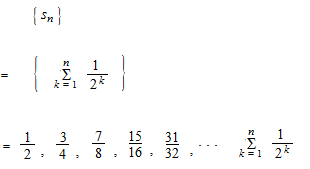
Séries
La limite de la suite des sommes partielles
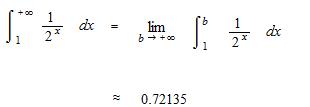
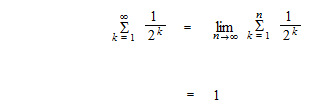
Ne confondons pas “la convergence de suite” et “la convergence de séries”.

Série télescopique
Très souvent, des calculs de série sont faits au moyen astucieux. Un exemple
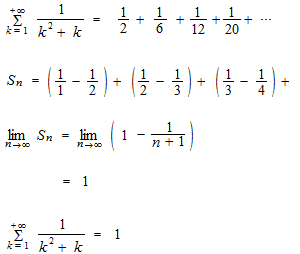
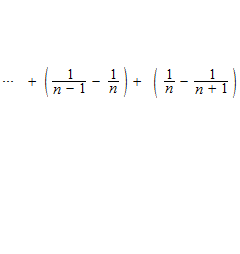
Série géométrique
On appelle suite géométrique une suite qui progresse à la raison fixe.
Une série géométrique est convergente, si sa raison r est − 1 < r < 1 .
Exemple
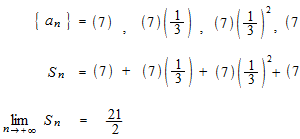
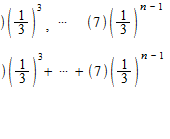
![]()
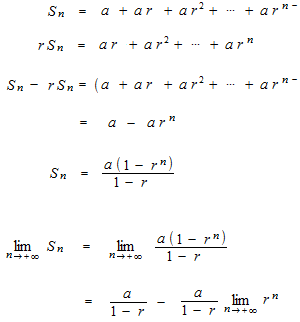
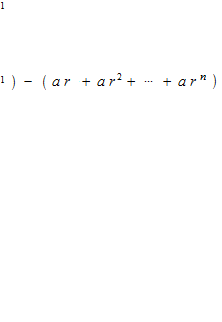
r = 1
Sn = a + a + a + ∙ ∙ ∙ + a = na divergente
r = − 1
Sn = a − a + a − a + ∙ ∙ ∙ + an divergente
La série harmonique
![]()
![]()
La série harmonique diverge.