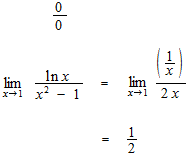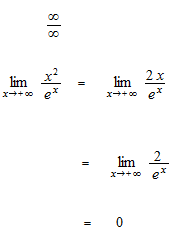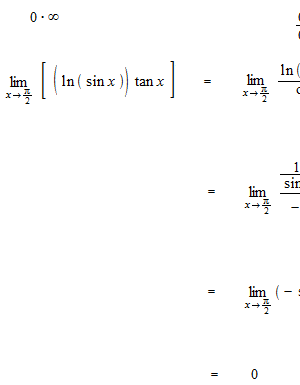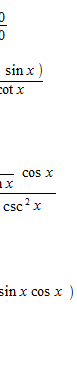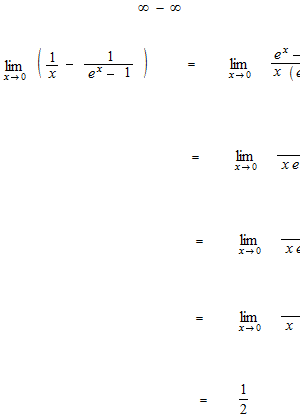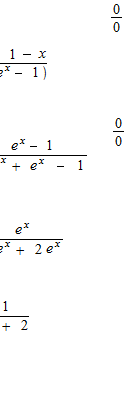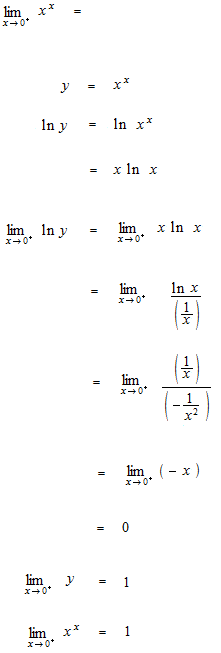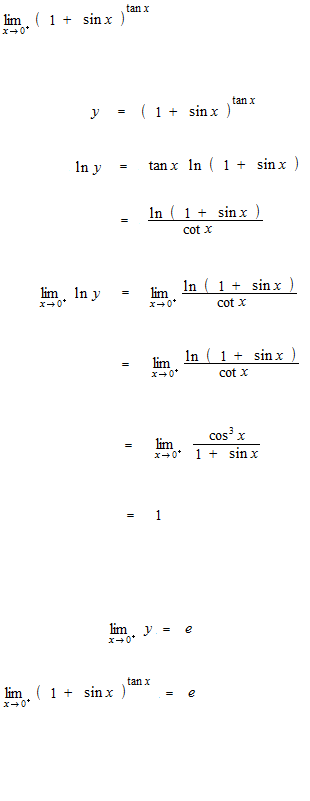L’Hôpital’s rule; proof
L’Hôpital’s rule is called sometimes L’Hospital’s rule. Graphical and intuitive understanding of the structure of L’Hôpital’s rule. L’Hôpital’s rule is, first, a very graphic conception. Delta-epsilon definition of L’Hôpital’s rule will be readily understood after a visual understanding. L’Hôpital’s rule can solve limit problem in indeterminate form, a function in fraction form of which numerator and denominator are both zero, 0 / 0 or both infinite, ∞/∞ at the limit point in question. L’Hôpital’s rule proof is very intuitive. It requires a graphical representation of derivative. How a derivative of function can be represented in a graph? A derivative is a tangent in all senses. A tangent is the proportion of some two values. In a coordinate system, this proportion is represented as inclinaition, then, after differentiation, as length. The unit “1” for proportion is not the same unit as the unite “1” for those two values. There must be another coordinate system on another squared paper. Length in a derivative graph is not quantity of things. Many confused questions come up from that confusion; Does dx have a certain length? etc..(dx can be a good quantity in terms of proportion. Very often, we use time-axis with dt. Some people apply time-axis to imaginary axis.) But graphics are, indeed, our great tool that can shows all kinds of values. We should freely make the most of their convenience and economize squared papers.
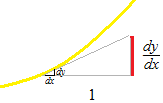
Tangent
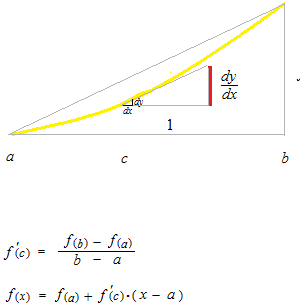
After a differentiation, which is done with the conception of the limit, a tangent is none other than a tangent at a point. We mustn’t say “very near the point p”, etc. A tangent can be mentioned only as slope of tangent line at a point. Let’s draw a length of proportion.
Mean value theorem of Lagrange
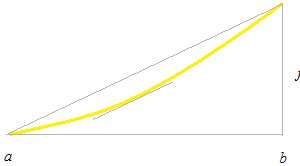
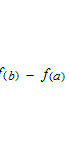
There necessarily exists at least one point where the slope of its tangent line is equal to the slope of the straight line passing through points a and b.
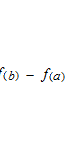

This equation will appear again in the next page as the two first terms of Taylor serie.
Mean value theorem of Lagrange can show the up and down of the curve with its derivative. The equation of mean value theorem justifies that the sign of derivative determines the up and down of the curve of its primitive.
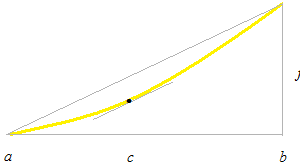
The triangle with base of length 1 and the triangle with base [ab] is not in the same coordinate system. The small triangle is not inside of the large triangle. Point c will be always between a and b even after limit operation and will be used as parameter value of derivative.


The combination of two curves of Lagrange’s mean value theorem is Cauchy’s mean value theorem.
L’Hôpital’s rule proof
We pull down f(a) and g(a) to 0.
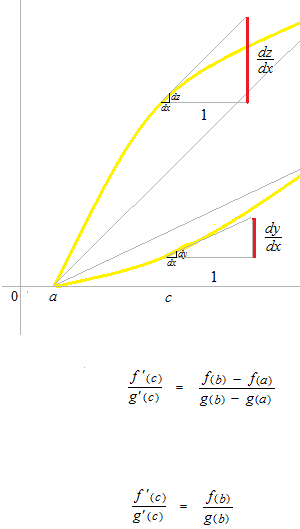
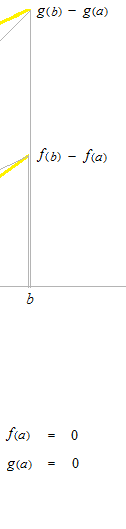
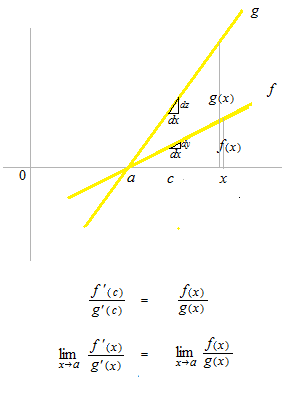
L’Hôpital’s rule of the case when it resolve the limit in indeterminate form
type 0 / 0 at c.
Figures of L’Hôpital’s rule in lateral and vertical symmetry with it will be treated in the same way.
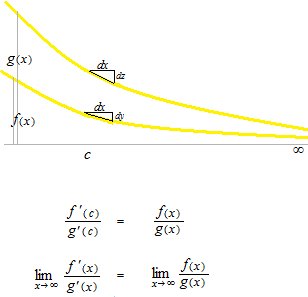
L’Hôpital’s rule proof of the case when it resolve the limit in indeterminate form
type 0 / 0 at infinity.
Figures of L’Hôpital’s rule proof in lateral and vertical symmetry with it will be treated in the same way.
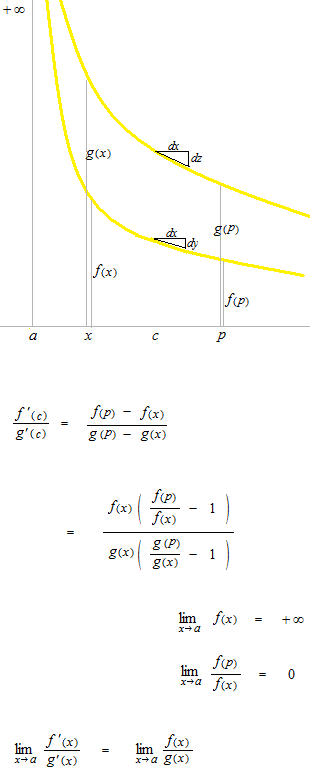
L’Hôpital’s rule proof of the case when it resolve the limit in indeterminate form type ∞/∞ at c.
Figures of L’Hôpital’s rule proof in lateral and vertical symmetry with it will be treated in the same way.
Some examples of operation with L’Hôpital’s rule