Arc cosinus, Arc cosinus, Arc tangente, Arc cotangente, Arc sécante, Arc cosécante
Fonctions trigonométriques réciproques
Arc sinus
Arc cosinus
Arc tangente
Arc cotangente
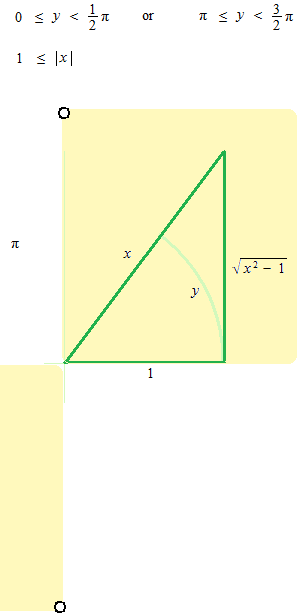
Arc sécante
Arc cosécante
Il y a deux façons d’écrire les fonctions trigonométriques réciproques.
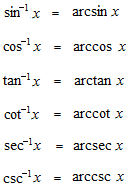
Les images, les domaines de définition et les dérivées des fonctions trigonométriques réciproques.
En tant qu’une fonction qui détermine une seule valeur d’image, une fonction trigonométrique réciproque doit être écrite toujours avec le domaine de définition. Chaque domaine de définition n’est que conventionnellement fixé.
Arc sinus,
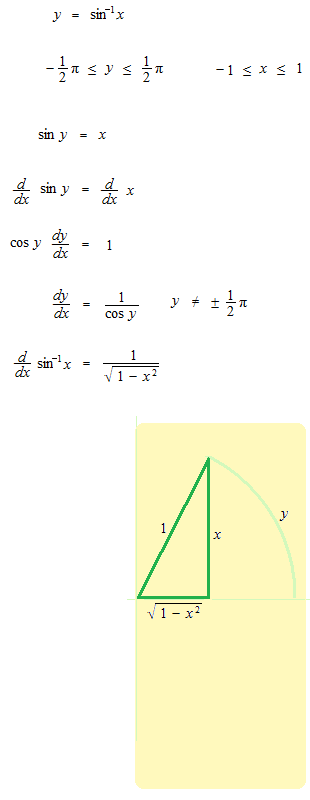
Arc cosinus,
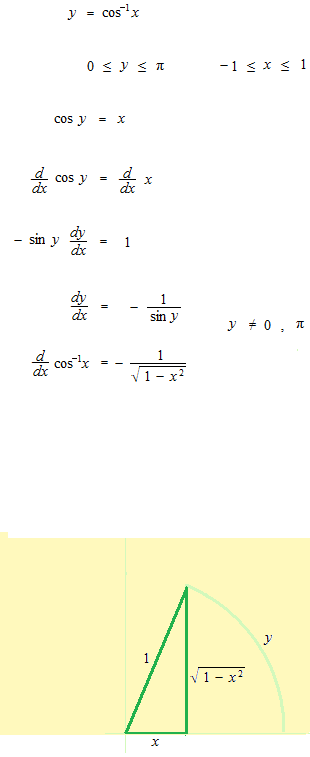
Arc tangente
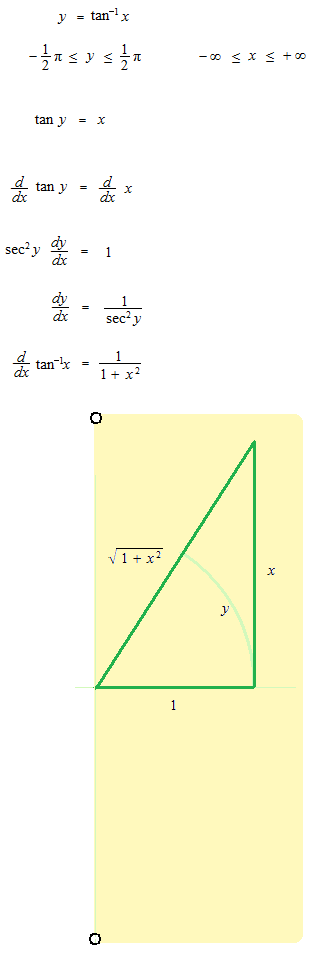
Arc cotangente
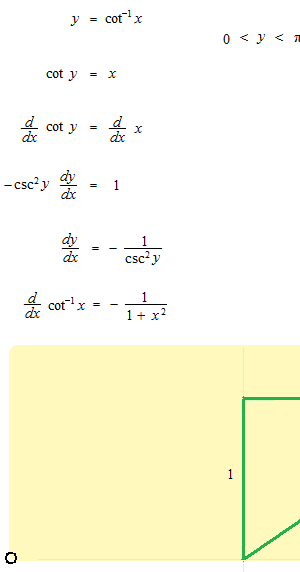

Arc sécante
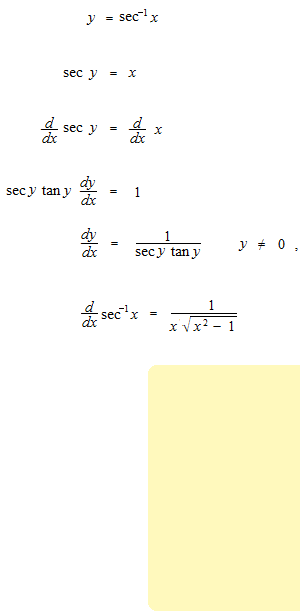
Arc cosécante
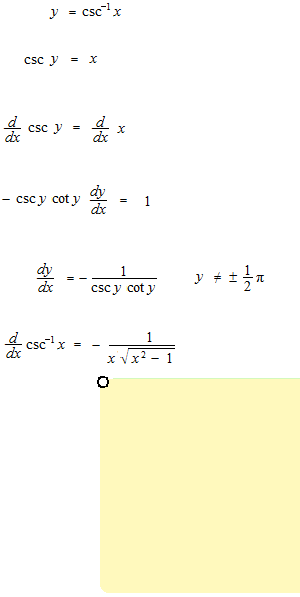
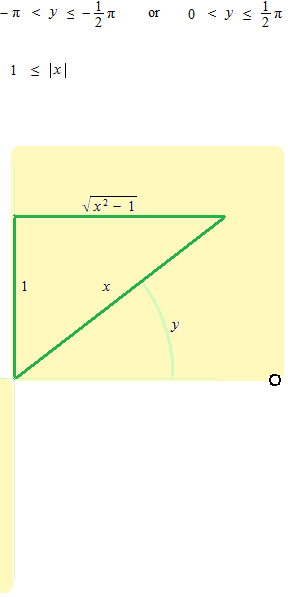
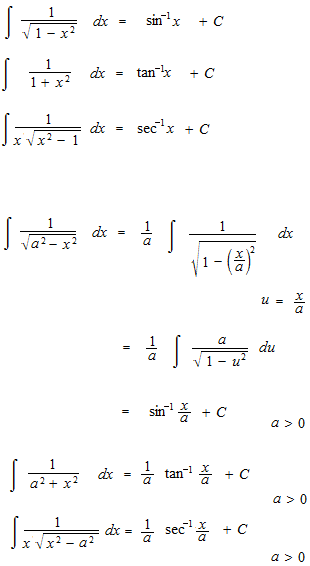
Examinez la longuer d’un quart de circonférence.

Voici, les graphiques partiels des six fonctions trigonométriques.
Si vous ne vous êtes pas encore familialisé avec ces courbes de fonctions trigonométriques, c’est le moment.
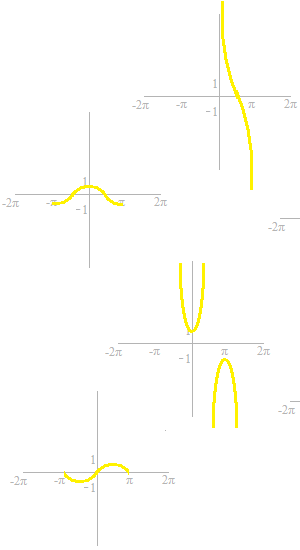
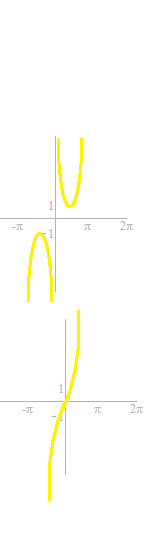
Pour regarder les fonctions réciproques, les droites y = x sont tracées.
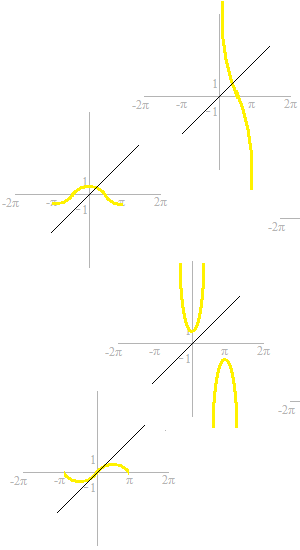
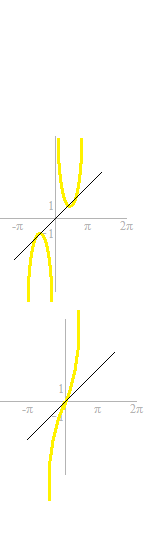
Les courbes qui sont symériques par rapport à y = x sont ajoutées.
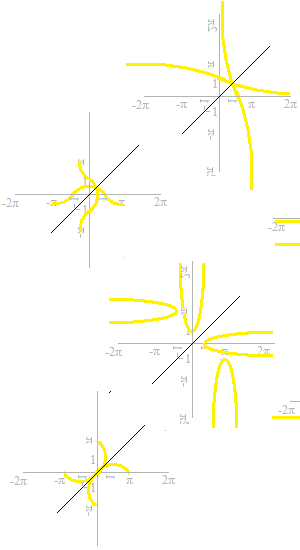
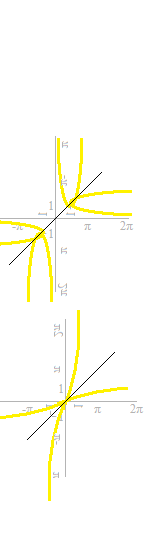
Quelques unes ne sont pas des fonctions.
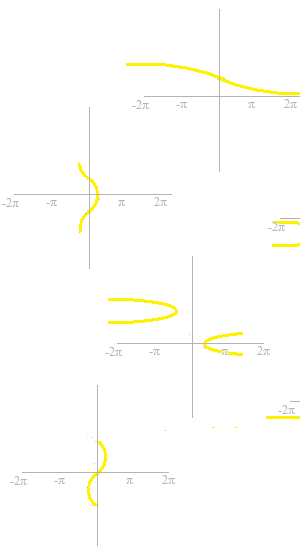
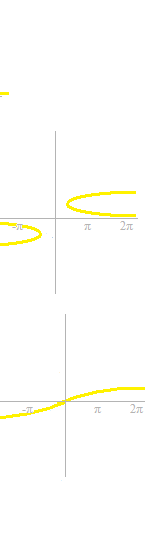
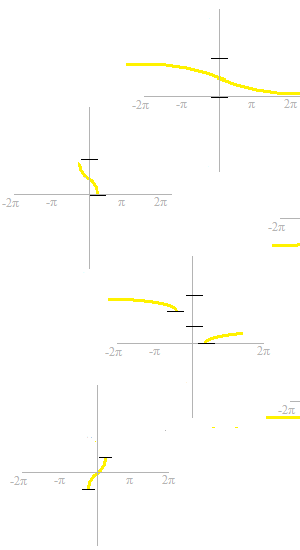
On élimine des parties dérangeante.
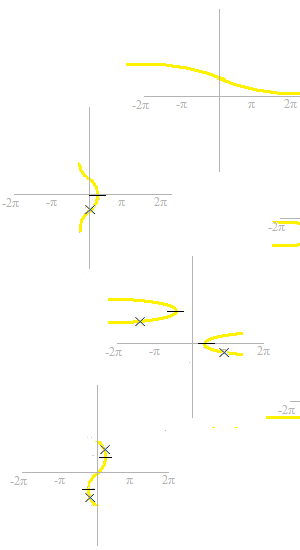
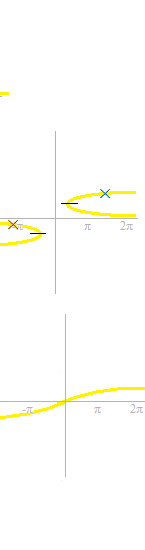
Maintenant, ce sont des fonctions.
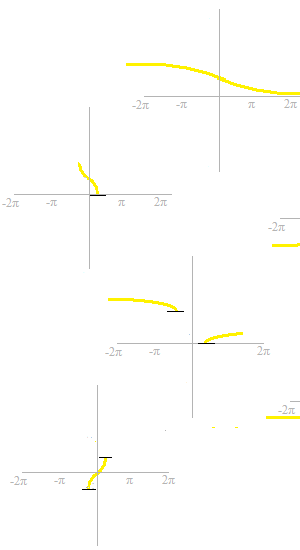

On ote aussi les parties correspondantes des fonctions trigonométriques.
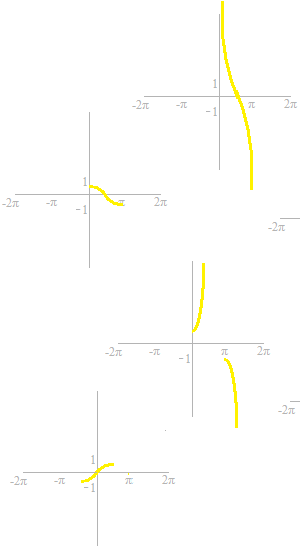
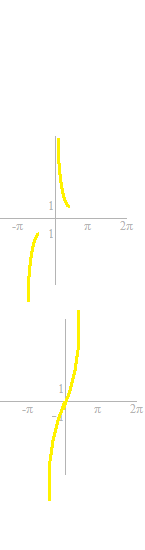
Arc cosinus, Arc cosinus, Arc tangente, Arc cotangente, Arc sécante, Arc cosécante,
