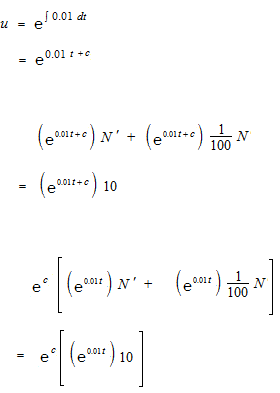Brine, first-order linear ordinary differential equation
In a large tank, there are 100 liter of pure water.
From a pipe which is above this tank brine is running into the tank 1l per minute.
At the same time, through a hole at the bottom of the tank, water flows out
also 1 liter per minute.
The brine contains 10 grams of salt per liter.
Find the amount of salt in the tank after 60 minutes.
Suppose that the solution in the tank is kept well mixed.
You have to consider the concentration of the flowing water is also increasing.
Statement is simple but difficult. The answer is 451,188 …gr. Let’s see the way to find the good answer.
Rectify the units
In the tank, there are always 100000 ml of water.
From the pipe, brine is running into the tank 1000 ml per minute.
Through the hole, water flows out also 1000 ml per minute.
The brine contains 10 grams of salt per 1000 ml .
Find the amount of salt in the tank after 60 minutes.
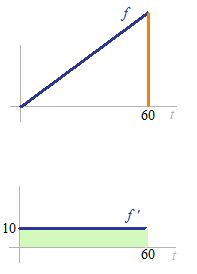
First, we are going to see only the coming-in salt.
Speed of the quantity of coming-in salt : f ‘(t) = 10
The amount of coming-in salt after 60 minutes : f (60)
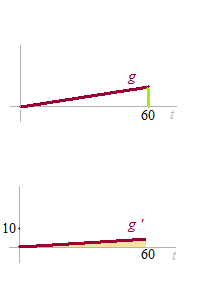
Now, we see only the going-out salt.
Speed of the quantity of going-out salt : g'(t)
The amount of going-out salt after 60 minutes : g(60)
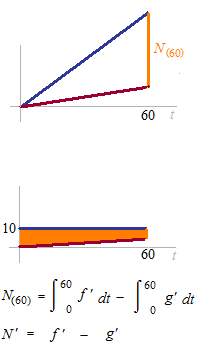
Total amount of salt in the tank N(t) = f(t) - g(t)
The rate of increase of the amount of salt
N'(t) = (speed of the amount of coming-in salt) – (speed of the amount of going-out salt)
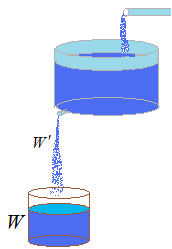
Speed of going-out salt g’ = ?
Amount of brine for t minutes. W(t)= 1000t
Speed of the quantity of brine at time t. W'(t)= 1000
Concentration of brinr in the tank at time t.
![]()
If the concentration is expressed in percentage, the value would be multiplied by 100 and this would complicate things. It is better to leave as it is. Speed of quantity of the going-out salt.
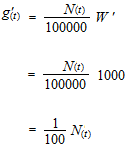
The words “per minute” tell you that it is already a derivative.
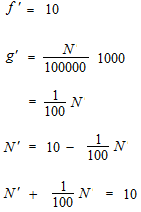
This is the differential equation which we were looking for.
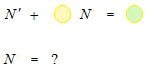
For a differential equation of this type, an integrating factor will work.
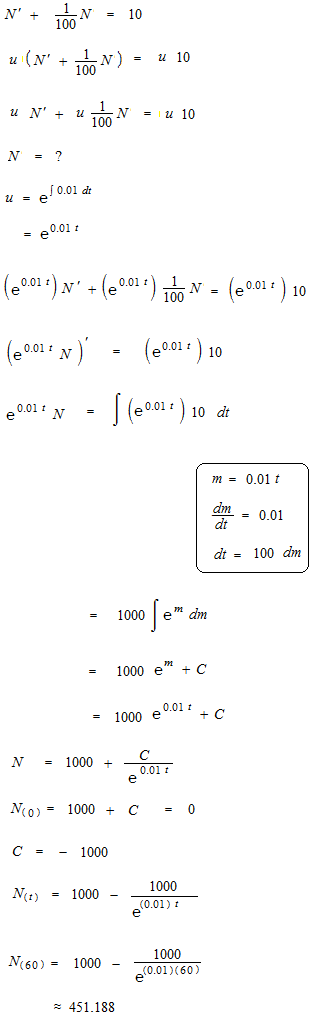
Constant of integration C of integrating factor will not be added. Normally constant of integration C must be written as an antiderivative will never be determinated after an indefinite integration. But constant of integration of integral factor can be eliminated as dividing both sides of the equation by ec beforehand.
Constant of integration C cannot be determinated arbitrarily. It is not possible to think as C = 0 without any condition. It is not possible to think either that you need only a single integral factor. It is important to consider that indefinite integral cannot be determinated as an absolute quantity as it is without condition.
It is only a simplification as dividing both sides by ec that constant of integration C of integral factor is not written. It is something very simple.