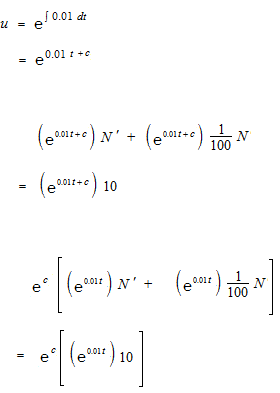L’eau salée. équation différentielle linéaire du premier ordre.
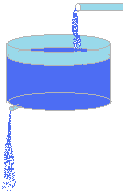
Dans un grand réservoir, il y a 100 litre d’eau pure.
Un tuyau qui se trouve au-dessus du réservoir verse de l’eau salée 1 litre par minute.
En même temps, en bas du réservoir, par un trou, l’eau du réservoir s’écoule également 1 litre par minute.
L’eau salée qui entre contient 10 grammes de sel par litre.
Trouver la quantité du sel dans le réservoir après 60 minutes.
Supposons que la solution dans le réservoir est maintenue bien mélangée.
On doit considérer l’augmentation de la concentration dans l’eau qui s’écoule.
Un énoncé simple mais c’est un problème difficile. La réponse est de 451.188…g. Nous allons regarder comment résoudre ce ploblème.
Rectifier les unités
time : minute
quantité d’eau salée : ml
quantité de sel : gramme
Dans le réservoir, il y a toujours 100000 ml d’eau.
Un tuyau verse de l’eau salée 1000 ml par minute.
Par un trou, l’eau s’écoule également 1000 ml par minute.
L’eau salée qui entre contient 10 grammes de sel par 1000 ml.
Trouver la quantité du sel dans le réservoir après 60 minutes.
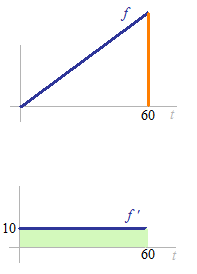
D’abord, on regarde seulement du sel qui entre.
La vitesse de la quantité du sel qui entre. f ‘(t) = 10
Le total du sel qui est entré pendant 60 minutes. f (60)
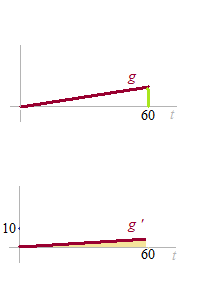
Puis, seulement du sel qui sort.
La vitesse de la quantité du sel qui sort. g'(t)
Le total du sel qui est sorti pendant 60 minutes. g(60)
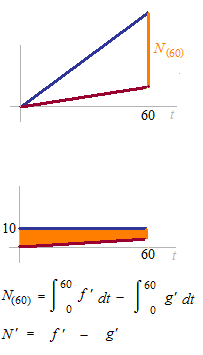
Le total de la quantité du sel dans le réservoir N(t) = f (t)- g(t)
La vitesse d’augmentation de la quantité du sel
N'(t) = (la vitesse de la quantité du sel qui entre)-(la vitesse de la quantité du sel qui sort)
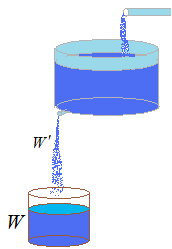
Vitesse du sel qui entre : g’ = ?
La quantité d’eau salée qui est sorti en t minutes : W(t)= 1000t
La vitesse de la quantité d’eau salée au moment t : W'(t)= 1000
La concentration de l’eau salée dans le réservoir au moment t .
![]()
Si l’on exprimait la concentration en pour cent, la valeur serait multipliée par 100 et cela compliquerait les choses. On fait mieux de laisser telle quelle.
La vitesse de la quantité de sel qui sort au moment t .
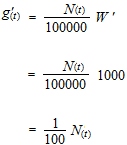
Les mots “par minute” you indique qu’il s’agit déjà d’une dérivée.
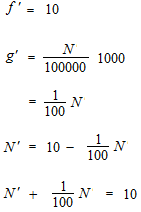
Ça c’est l’équation différentielle qu’on a attendu.
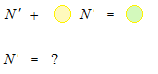
Pour une équation différentielle de ce type, on utilise le facteur intégrant.
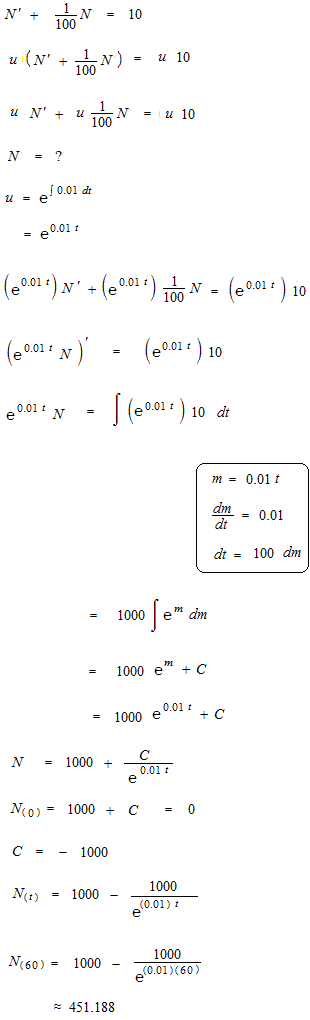
La constante d’intégration C de facteur intégrant n’est pas ajoutée par convention. Normalement la constante d’intégration C doit être toujours marquée comme la primitive ne sera pas déterminée après une intégration indéfinie. Mais la constante d’intégration de facteur intégrant peut être éliminée des deux côtés d’équation par anticipation.
La constante d’intégration C exprime n’est jamais déterminée arbitrairement. Il n’est pas possible de penser sans condition comme C = 0. Il n’est pas possible de penser comme il suffit d’avoir un seul facteur intégrant non plus. C’est essentiel de considérer que l’intégrale indéfinie n’est pas déterminée comme une quantité absolue.
C’est seulement pour la simplification en divisant deux côtés par ec que la constante d’intégration C de facteur intégrant ne sera pas écrite. C’est quelque chose de très simple.