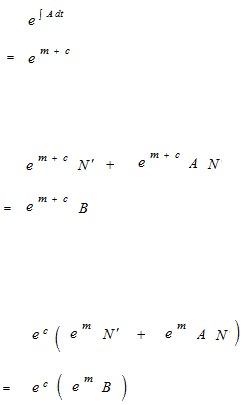Integrating factor; Constant of integration
Integrating factor for first-order linear ordinary differential equation.
Here is an useful tool called integrating factor. You will be able to change a certain differential equation,
N ‘ + k N = A
which contains a derivative, into a normal algebraic equation as multiplying each side of equation by integrating factor.
Before explaining what integrating factor is, let’s see what it can do.
The next page of this site will present you a problem of brine in which there will be a differential equation like this.
Answer must be N(t) = ?
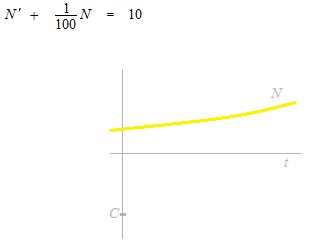
If the question were N’ = 10, the answer would be N = 10 t + C
But there is some small quantity with it.
When you multiply the both sides of this differential equation by e0.01t, you will know what was the equation in normal form, an algebraic equation.
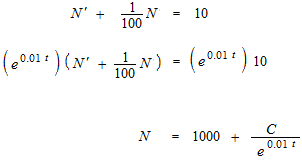
This will be explained below.
Integrating factor is very useful. Here is the explanation.
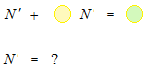
An integrating factor is used to eliminate the derivative of a differential equation in a shaped like this , first-order linear ordinary differential equation, and make it in normal form , an algebraic equation.
Here, N(t) expresses a certain increasing quantity.

To remove N’ , you could do an integration both sides of this differential equation, but, at the same time, it would make an integral of N too. As you want to find what N is, you will differentiate the equation and you will make N’ again.
There was someone who found a way to eliminate N’ using the fact that N can be a part of the result of a differentiation with chain rule.
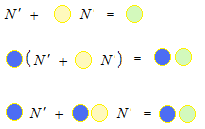
You multiply both sides by the integrating factor.
Let’s stop using color balls and use alphabet.
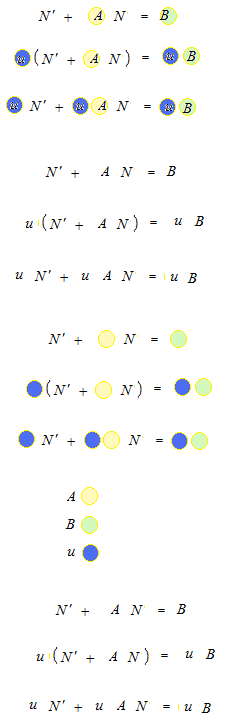
Suppose that u is something nice which can make uB the result of a differetiation of uN .
Let’s differentiate uN .
Chain rule
If u’ is uA , you can make it in form of N = ……

In order that u would work like this, what u must be ?
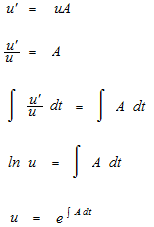
This u is called integrating factor for first-order linear ordinary differential equation.
Constant of integration C of integrating factor will not be added. Normally constant of integration C must be written as an antiderivative will never be determinated after an indefinite integration. But constant of integration of integral factor can be eliminated as dividing both sides of the equation by eC beforehand.
Constant of integration C cannot be determinated arbitrarily. It is not possible to think as C = 0 without any condition. It is not possible to think either that you need only a single integral factor. It is important to consider that indefinite integral cannot be determinated as an absolute quantity as it is without condition.
It is only a simplification as dividing both sides by eC that constant of integration C of integral factor is not written. It is something very simple.