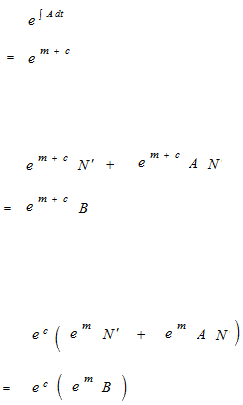積分因子の積分定数C
積分因子の理解は自分で書きながらのほうが納得しやすいはずです。
積分因子の数を式の両辺に掛けることによって導関数が混ざった式、
1階線型常微分方程式
N ‘ + k N = A
を解くことができます。
以下はその説明ですが、まず、積分因子の例を先に見てしまいます。
あとで扱う塩水の問題では下のような式が出てきます。
この式から N(t) = ?という答を出します。
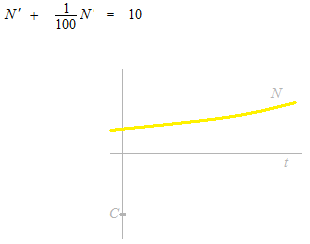
もし N’ = 10 という問題だったら答は N = 10t + C ですが、
もう少し何かがついています。
この場合の積分因子は e0.01t です。この導関数が 混ざった式の場合、
両辺に積分因子の e0.01t を掛けると式の正体が分かります。
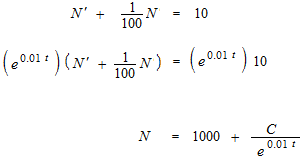
これが答ですがなぜでしょうか。パズルのようなものですが、
これから説明します。
これがどういう話かはあとで扱う塩水の問題で明らかとなります。
積分因子はこのようなかたちの微分方程式、1階線型常微分方程式を解くときに使います。
積分因子のタネ明かしは以下の通りです。
積分因子の対象となる式はこのような形の式です。
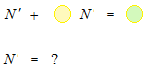
導関数が混ざっている変な式から導関数をなくして、普通の式、代数方程式、にしたいわけです。
変数に N という文字を用いているのは時間とともに増えつつある物や減りつつある物の数 number というような意味ですが、勿論 yでも何でも結構です。

N’ をなくすには全部積分してしまえばよいのですが、求めている Nそのものまで積分してしまって、それではその Nは何かというときに、また全部微分したら、またN’ ができそうです。これではいけません。
N’ が Nをチェーンルール で微分した結果であるということをそのまま使う方法を発見した人がいたようです。
両辺に積分因子の数を掛けます。
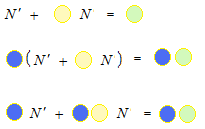
色の玉を使うのをやめて、アルファベットにします。
積分因子のアルファベットは uにします。
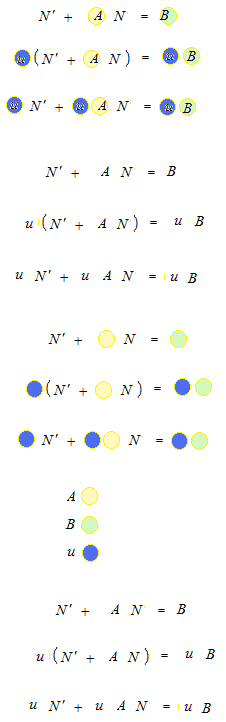
積分因子 u の理解は自分で紙に書きながらしましょう。
ここで、uBが uN を微分した結果だとします。
uN を微分してください。

チェーンルール
積分因子の由来は チェーンルールにあります。
もしも、 u’ がuA ならば N = ….. の形になるところを見ましょう。
そのような u とはどのような uでしょうか。
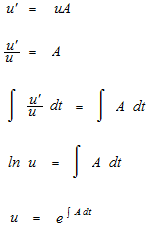
自分で紙に書いて覚えましょう。覚えてしまったら、次のページで塩水の問題で使い方を見ます。
積分因子の指数の部分には積分定数 C は慣習としてつけません。積分定数 C は原始関数が限定されないことを表しているので不定積分には必ず書かれなくてはいけません。しかし、積分因子の場合は積分定数 C は両辺を ec で割れるので前もって簡略にします。
積分因子の指数の部分には積分定数Cは不必要なため昔から慣習として公式にはつけないことになっています。Cは決して任意に無条件で限定されることがないので C = 0 と考えたり、積分因子はひとつを選べばそれで足りるといった考えは、不定積分はそれ自身では絶対的な量としては不定であるという本質を無視した考えです。前もって両辺を ec で割るというのが積分定数を書かない理由です。とても単純な理由です。