Law of heating of Newton
Normally, this law is called law of cooling as generalizing all cases, not law of heating.
Anyway, and therefore, as a law, it should be able to be used with negative values. But you might feel some complexity to handling the curve of exponential function. Is it necessary put minus sign somewhere?
Law of cooling de Newton for a case of heating .
Surrounding temperature is at 0°C. An even colder object gets closer to 0°C.
That is the same curve as bank interest, exponential function, but the time is backward and also the temperature on vertical axis is opposite.
Negative value of time can be also expressed by negative value of k as the previous page.
N= N0 ekt
t ≤ 0 , k ≥ 0 ≡ t ≥ 0 , k ≤ 0
Then the curve is vertically opposite. Temperature of object converge from N0 to 0 .
N= N0 ekt k ≤ 0 N0 ≤ 0
If it were a bank, it would be a banc of which the interest is negative. When you borrow money, you will owe less and lass.
A is not always 0°C. Generalized form of the law of cooling.
N − A = ( N0− A ) ekt
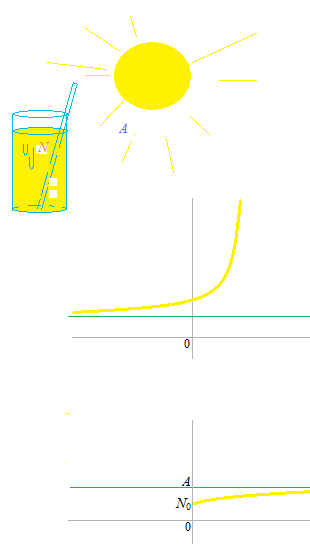
A glass of orange juice without ice : N ° C.
Initial temperature : 2°C.
Ambient temperature: 32 ° C
After 8 minutes, the temperature of orange juice rose to 6 ° C
Find the temperature of orange juice after 15 minutes.
It is possible that N would go up heigher than A . But here, we consider this problem like this graph.
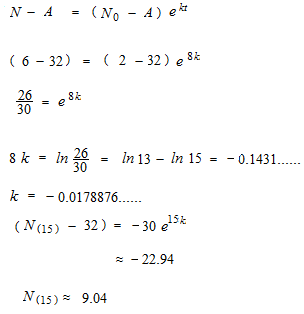
Calculation of differential equation is already included in the formula of the law of cooling. To find answer of problem, calcul of integral is not used.
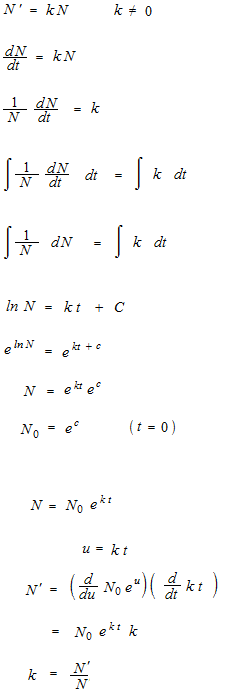
Reverse
