La loi de réchauffement de Newton
Normalement, on appelle cela la loi de refroidissement plustôt que la loi de réchauffement comme la formule de la loi de refroidissement est valable aussi pour un réchauffement. Comme c’est une loi, elle devrait être utilisée avec des valeurs négatives par-ci par-là. Mais, il y a une complexité au niveau de la compréhension de la coube de fonction exponentielle.
Est-ce qu’on doit mettre le signe négatif ‘ − ‘ quelque part dans la formule?
La loi de refroidissement de Newton. Dans le cas d’un réchauffement.
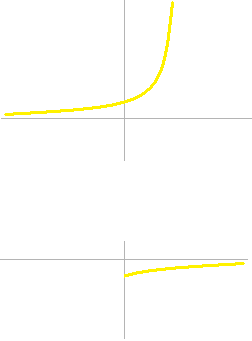
D’abord, la température ambiante est à 0°C et un objet qui est encore plus froid s’approche de 0°C en montant.
C’est la même courbe que celle d’intérêt de banque, mais le temps est à l’inverse et l’axe vertical de température est aussi à l’inverse.
Pour l’inversion du temps, on peut considérer aussi que c’est le coefficient k est négatif comme la page précédente.
N= N0 ekt
t ≤ 0 , k ≥ 0 ≡ t ≥ 0 , k ≤ 0
En suite, l’inversion sur l’axe vertical. La température d’objet converge de N0 vers 0 .
N= N0 ekt k ≤ 0 N0 ≤ 0
Si c’était une banque, ce serait une banque qui mettrait un intérêt négatif. Vous avez emprunté de l’argent et vous avez de moins en moins de débit au fil du temps.
Température ambiante n’est pas toujours à 0°C. Généralisation de la formule.
N−A= (N0 −A)ekt
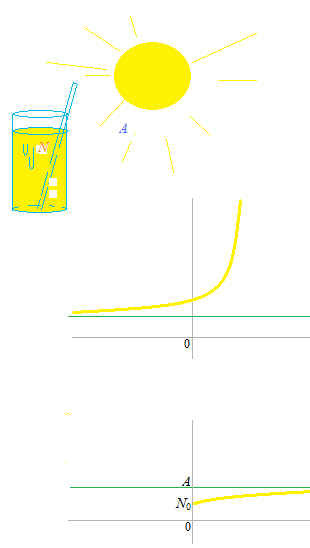
Un verre de jus d’orange froid sans glaçons N ° C.
Il était à 2 ° C au début.
Température ambiante : 32 ° C,
8 minutes après, la température de jus d’orange est à 6 ° C,
Calculez la température de jus d’orange après 15 minutes.
Eventuellement, au fil du temps, N pourrait monter et dépasser A. Mais, ici, nous considérons ce problème comme ce graphique ci-dessus.
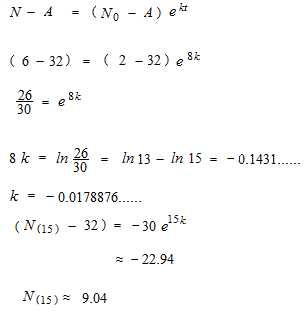
La maniére de résolution d’équation différentielle est déjà inclue dans la formule de la loi de refroidissement de Newton.
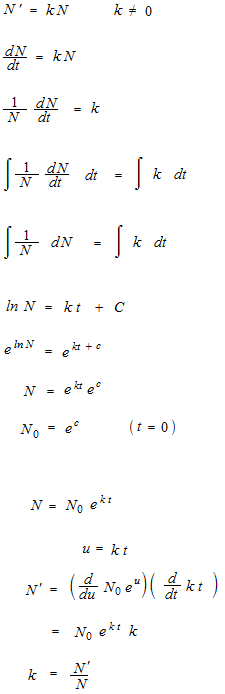
Dans le sens inverse
