Loi de refroidissement de Newton
Décroissance exponentielle
Il s’agit de la courbe de température d’une chose en refroidissement qui a N °C dans la température ambiante de A°C . A peut être une tempéraure négative. C’est après le résultat des observations qu’on dit que cette loi est bonne. En réalité, il y a quelques influences de la part de l’aire de la surface et la nature de la matière. Ici, le coefficient k comprend tous ces coefficients.
D’abord, le cas où la température ambiante est à 0°C . C’est la même courbe que celle de l’intérêt de banque. Une fonction exponentielle. Mais le temps est à l’inverse.
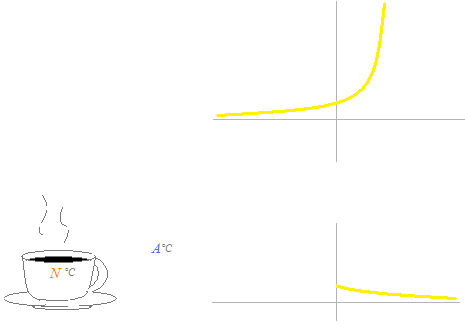
N = N0 ekt
t ≤ 0 , k ≥ 0 ≡ t ≥ 0 , k ≤ 0
Ou bien, si c’était une banque, ce serait une banque qui mettrait un intérêt négatif. Le créancier aurait de moins en moins de solde.
Comme A n’est pas toujours à 0°C, nous allons généraliser
N − A = ( N0− A ) ekt
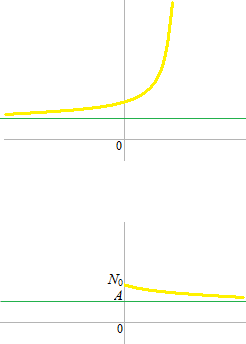
La manière de translation de courbe.
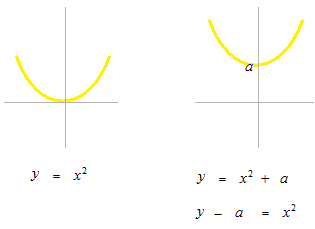
Un café de 90 ° C refroidisse dans une chambre où la température ambiante soit de 25 ° C. Si, après cinq minutes, la température du café est à 75 ° C, calculez la temperature du café après 10 minutes.
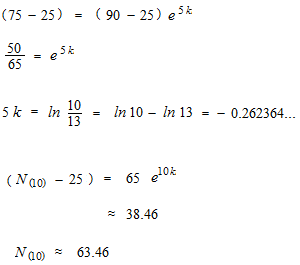
La solution de fonction différentielle, c’est-à-dire l’intégration, est déjà inclue dans la formule. L’intégration n’est pas utilisée pour trouver la réponse.
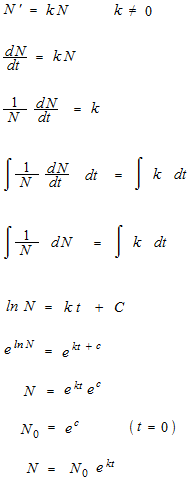
Dans le sens inverse.
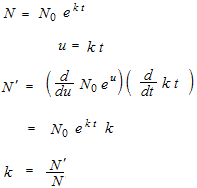
Loi de refroidissement de Newton
