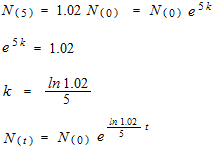First-order linear ordinary differential equation; Bacterial growth
When we say equations, that means algebraic equation. An algebraic equation may have three, four terms. If you consider one of terms, or two, as a derivative, that function can be also a differential function.
For example, an algebraic equation with distance y and velocity v .
A car runs a distance of 200km from the starting point.
vt = 200
If you consider the verocity as a derivative, this equation can be a differential equation.
y’t = 200
The solution of a differential equation is done by writing the antiderivative y = of the derivative y’
y = 200
Between an algebraic equation and a differential equation, there is no difference. Only the answer of a differential equation is the antiderivative of a term, when you consider this term is a derivative.
Normally, when you do an integral operation, there must be a derivative somewhere.
The question is to find the use of derivative.
Here, in these several pages, we are going to see some classic problems.
Separable first-order ordinary differential equation
N ‘ = k N
Bacterial growth
Newton’s law of cooling
Canbon 14
First-order linear ordinary differential equation
N ‘ + k N = A
Brine
Integrations of differential equations are puzzles. Here is a constant function. If you think this function is the expression of a slope, it can be also a differential equation. Write a linear function doing an integration in this way.
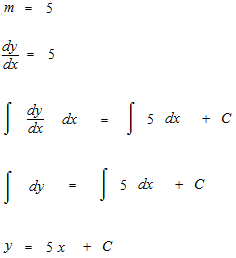
Another constant function. You think this one expresses the acceleration of free fall.
The integration will be done like this.
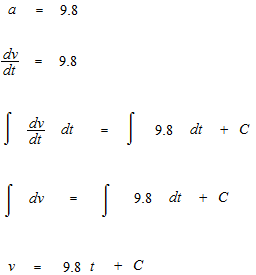
N = N0ekt
This formula has no term which can be considered as a derivative of N .
The next form is a differential equation.
N ‘=kN
But in order to find answer of question, as the differential function is already included in the formula, you don’t need to use differential function.
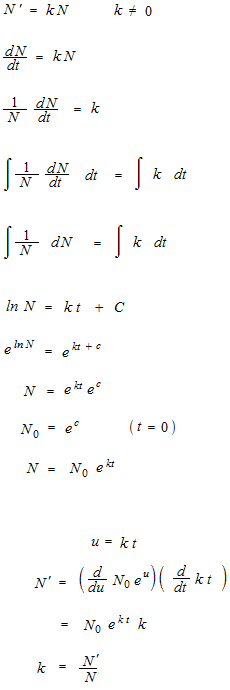
Bactrial growth
It is a result of observations that certain bacterial growths are expressed by courbe of exponential growth. Otherwise it is a pure hypothesis for an example to study exponential function. There is no mathematical necessity in it.

A certain bacteria double in 2 hours, how much time does it take to triple?
t : hours
N(t) : quantity of bacteria
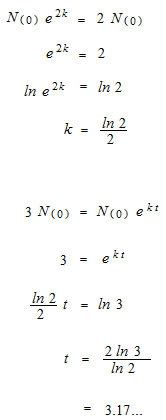
Certain bacteria multiply by 2% every 5 minutes. Find the number after t minutes.
t : minutes