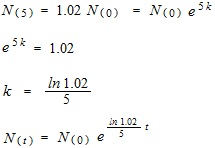Prolifération des bactéries; Équation différentielle ordinaire à variables séparables.
Quand on dit des équations, il s’agit normalement des équations algébriques. La plupart du temps, une équation se compose de quelques termes. Si l’on considère un terme, ou deux, d’une équation algébrique comme une dérivée, cette équation pourra être appelée aussi une équation différentielle.
Par exemple, une équation y de distance et de vitesse v .
Une voiture qui parcoure la distance de 200km à partir du point de départ.
vt = 200
Si l’on considére la vitesse comme la dérivée de la distance, cette équation sera considérée comme une équation différentielle.
y’t = 200
Résoudre une équation différentielle veut dire de chercher la primitive y = de cette dérivée y’ .
y = 200
Une équation peut considérée comme algébrique et comme différentielle en même temps. Si l’on considére un terme comme la dérivée dont on cherche la primitive, c’est une équation différentielle.
Quand on fait une intégration, cela veut dire qu’on a trouvé une dérivée qualque part. La question est de trouver la dérivée dans une équation algébrique.
Ici,en quelques pages, nous allons voir des problèmes classiques.
Équations différentielles ordinaires à variables séparables du premier ordre
N ‘ = k N
La prolifération des bactéries
Loi de reffroidissement de Newton
Carbone 14
Équation différentielle linéaire du premier ordre
N ‘ + k N = A
L’eau salée
Intégations comme solutions d’équations différentielles sont des puzzles.
Soit une fonction constante. Vous pensez qu’elle exprime l’inclinaison d’une courbe. Ce sera une équation différentielle, si l’on cherche cette courbe, la primitive.
Voici, la manière d’intégration.
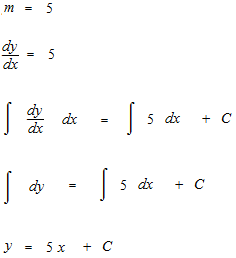
Soit une autre équation constante. Vous pensez que c’est l’accélération de la chute libre. Vous considérez cette équation comme une équation différentielle.
Voici, l’intégration.
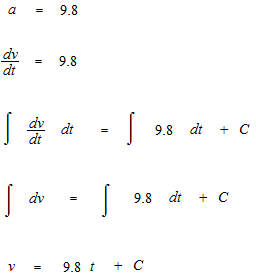
N = N0ekt
Cette formule de l’intérêt de banque ne peut pas être une équation différentielle de N comme il n’y a pas de N’.
L’autre forme est une équation différentielle.
N’ = kN
Pour résoudre des problémes, comme la fonction différentielle est déjà inclue dans la formule, on n’utilise pas la fonction différentielle.
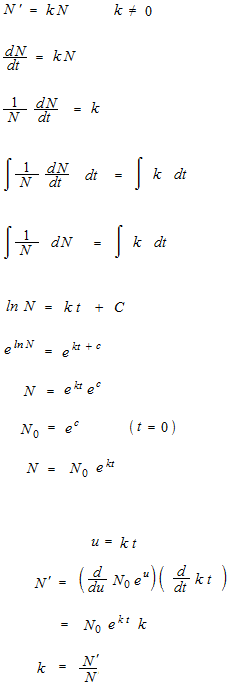
La prolifération des bactéries
C’est le résultat d’observation qui détermine si une certaine bactérie prolifère en équation différentielle ordinaire du premier ordre. Sinon une hypothèse pour donner un exemple probable d’équation différentielle ordinaire du premier ordre. Ce n’est pas une nécessité mathématique.

Une certaine bactérie prolifère double en deux heures. Elle met combien de temps pour tripler.
t : heures
N(t) : nombre
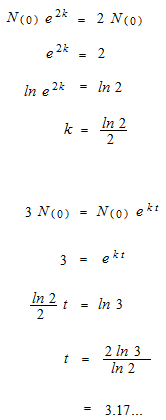
Une certaine bactérie prolifère 2% en 5 minutes. Trouvez le pourcentage après t minutes.
Croissance bactérienne