連続複利
対数は、増え方が速くて、すぐに天文学的な数になってしまうような気がしますが、実際に使われる場合は利息の計算のように、きわめて小さな割合でとても緩やかな曲線で繊細に扱われます。指数関数的増加、指数関数的減少など、むしろ少しずつ変化していくものの計算に、まるで足し算のように使われるともいえます。
y = logbxを 「 xはbの y乗です。」と読めたら対数の足し算、掛け算などはそのままできます。
まず対数の簡単な例として十二音の平均律の半音の比率の計算です。
十二音の平均律
平均律は低音域、高音域には向きませんが、中音域では今の私たちの耳にここちよく響きます。平均律はバッハの時代に計算されました。平均律の三度、六度のうなりは美しくふるえます。四度、五度も動きがあります。十二音的な感覚の音楽も平均律そのものの美しさが土台となります。
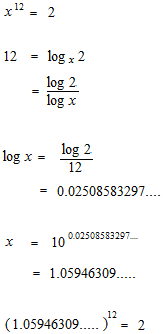
平均律ではひとつの音の振動数に 1.05946309….. を掛けると半音上がります。
利息
お金の計算をするために数学を学ぶわけではないので利息の計算には興味が沸かないかもしれませんが、利息の計算は対数のグラフの曲線の構造を理解するためにはなくてはならない例題です。
以下の説明に於ける銀行は出鱈目の銀行ですから、とんでもない利息がつきます。また、最初に元金を預けてから後は、もうお金の出し入れはありません。
連続複利と呼ばれますが、実際の銀行では365日で計算しているようです。
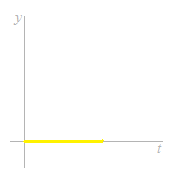
預けた金額が0円のときは利率がどうであれ、いつまで待っても利息はつきません。対数の曲線には、横軸に触らないという大きな特徴があります。
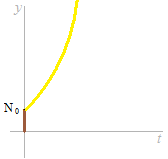
最初は0からは始まりません。或る金額が必要です。
最初の金額、元金を N0とします。
横軸はt
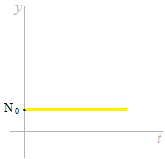
利息が0の場合は増えません。
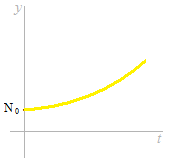
利息の率が低い場合は増えかたが少ない。増えかたの増えかたが遅い。
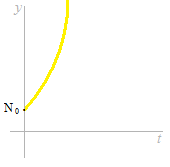
利息の率が高い場合は増えかたが多い。増えかたの増えかたが速い。
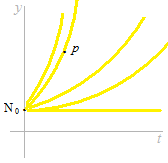
N0 が定まっているとき、別の一点 pを通るための利息はひとつしかありません。
二点を通る利息はひとつしかありません。
曲線が決定されると、導関数も決定されます。
例えば点 ( N0 , 0 ) に於ける傾きもひとつだけ決定されます。
最初にいくら預けて、それがいついくらになったかが分かると利息が分かります。
太郎さんが銀行に元金100000円を預けて1年間忘れていたら200000円になっていました。この気前の良い銀行の利息はどのくらいでしょうか。
ただし、年利の365分の1が毎日加算されるとします。
年利 ; k
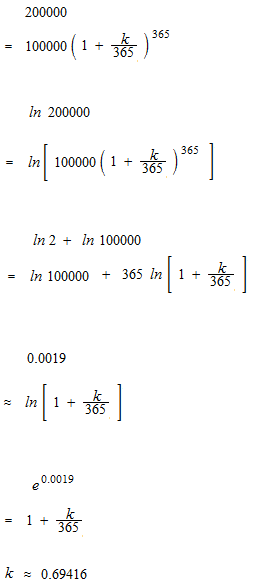
y = ln xを 「 xは eの y乗です。」と読めたら対数の足し算、掛け算などはそのままできます。
定数項は電卓を使います。
年利の365分の1が毎日加算されるとき、年利69.416%で2倍になります。
別の銀行。もっと気前がよくて年利100%です。
年利100%では元金100000円は一年後いくらになるでしょうか。
年利の365分の1が毎日加算されるとします。
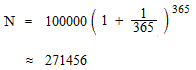
毎時間加算される場合、
年利100%では元金100000円は一年後いくらになるでしょうか。
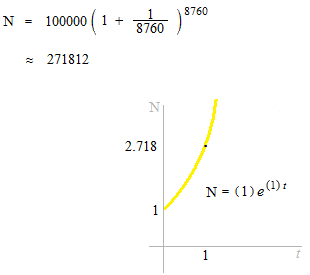
1円を年利100%で1年間無限に細かく加算すると2.718…..円になり、この数字がe自然対数の底と呼ばれます。
( 0 , 1 ) , ( 1 , e )を通る利息の曲線は一本しかありません。
銀行預金の公式
N = N0 e k t
k年利
t年間
実際の銀行では年利は 2% ぐらいでしょうか。
0.02 とします。1.02 とはしません。
さらに別の銀行。
太郎さんがある銀行に1円預けて1年間忘れていたら2円になっていました。この銀行の利息はどのくらいでしょうか。無限に細かく加算されるとします。
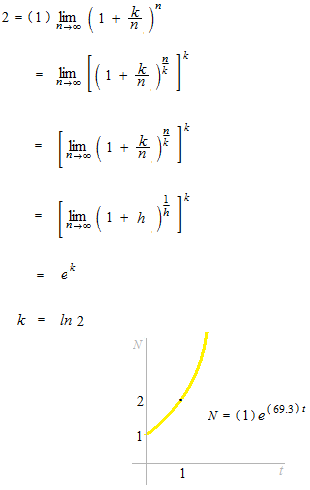
年利 69.3…% で1年で 2倍になります。
( 0 , 1 ) , ( 1 , 2 ) を通る利息の曲線は一本しかありません。
利息 kが 100% の場合、一年後には 2 倍ではなく 2.718 倍になります。
はたして利息 kとは何なのでしょうか。
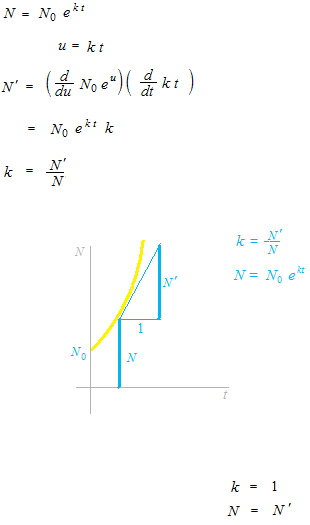
k は N と N’ の比率です。
上のグラフの中の1は N’をタンジェントとしたときの1です。k ではありません。
N’ = kN
N = N0 e k t
このふたつの式は同じことをいっています。
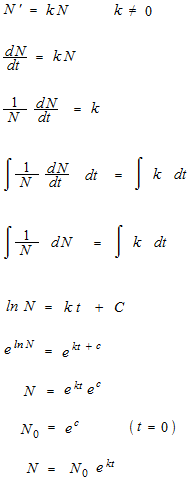
逆方向
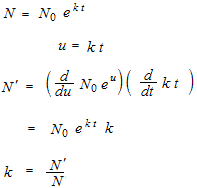
y'(t)=y(t)
y =
答えは y =et ではありません。
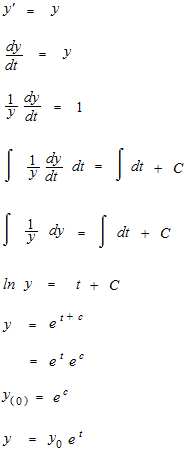
指数関数の感覚がつかみにくい場合、直感的につかむために無理矢理十進法と桁数にしてしまってもいいかもしれません。桁数は勿論整数ですが、これをもしも連続していたと想像して横軸 tとします。
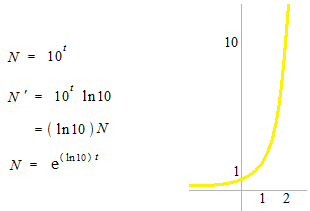
一年たつと10倍になる銀行の利息は (100) (ln 10) % です。
指数関数はe進法です。桁数は整数ですが、これをもしも連続していたとして横軸 tとします。
直感的につかむために2.718進法といってしまいます。
初期条件 N0 は初期条件が1の指数関数と同じ形で縦軸の単位1の代わりに N0 にすると考えることもできます。

指数関数的増大は、或る時点での量とその時の導関数との率が一定であるような関数です。
