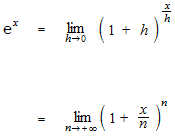Nombre népérien 2.718…. ou constante de Napier ou de Néper.
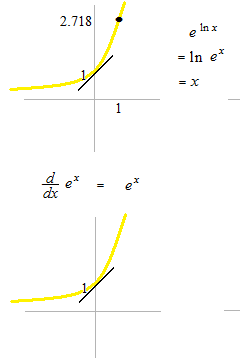
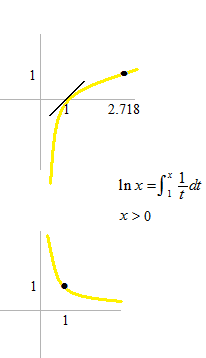
Les lignes tangentes sont d’inclinaison 1.
La fonction exponentielle est sa dérivée sont identiques.
La fonction exponentielle et la fonction logarithme naturelle sont réciproques.
La fonction logarithme naturelle est définie par la fonction inverse.
Le nombre qui satisfait ces relations entre quatre fonctions est le nombre népérien.
Il n’y a pas de relation directe entre la dérivée de la fonction exponentielle et la fonction inverse.
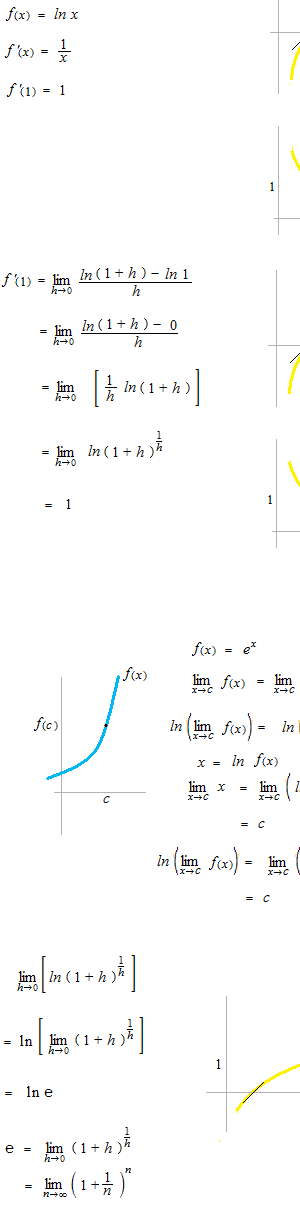
La différentiation de la fonction logarithme neturelle.
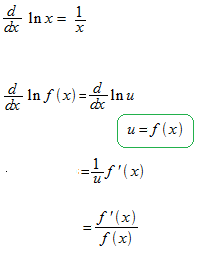
Le signe de value absolue est utilisé à la integrale indéfinie de la fonction inverse.
![]()
À droite de signe log ou ln est toujours une valeur positive.
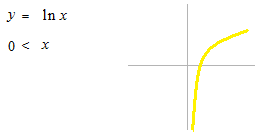
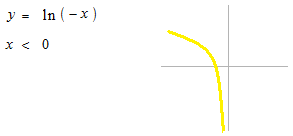
Donc il est bien possible d’écrire comme ceci.。
Deux expressions peuvent être écrites ensemble.
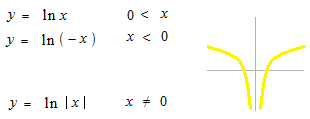
Différentiation
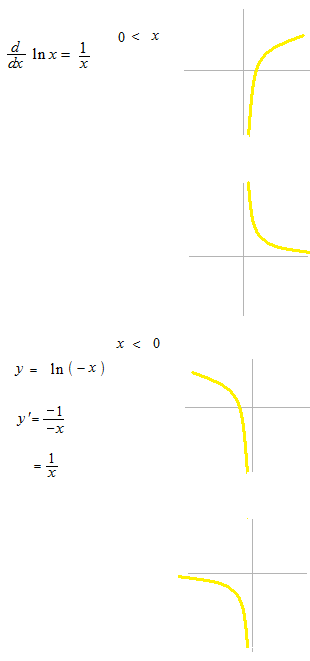
Deux expressions peuvent être écrites ensemble.
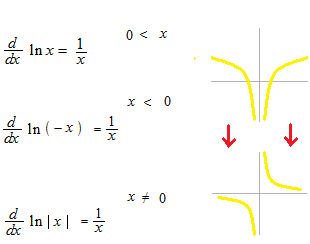
Intégrale indéfinie.
![]()
Un exemple de différentioation avec la fonction logarithme natuerelle.
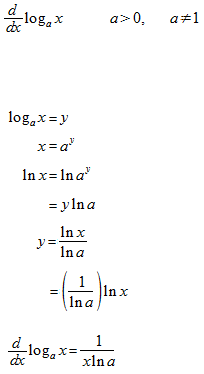
Un exemple de différentioation avec la fonction logarithme natuerelle.
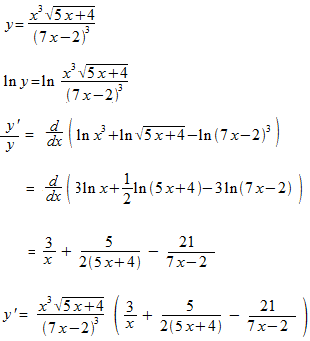
Différentiation des fonctions exponeltielles.
En utilisant les formules de defférentiation de la fonction lagarithme naturelle, on fait des différention des fonctions exponentielles.
La base est un nombre réel.
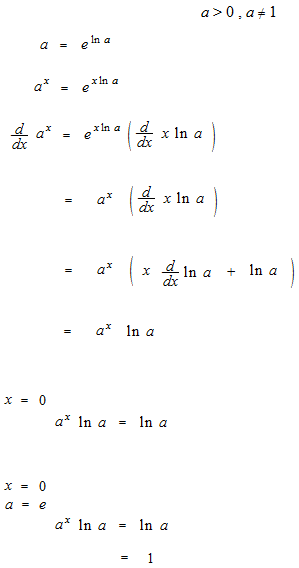
Si la base n’ est que e , la différentiation est beaucoup plus simple.
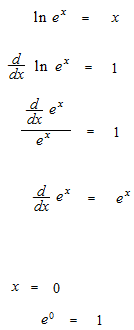
Un exemple de différentiation de fonction exponetielle.
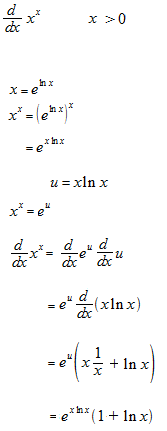
Un autre exemple de différentiation de fonction exponetielle.
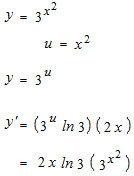
Intégrale de fonction exponentielle.
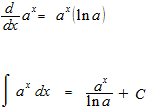
Un exemple de l’intégrale de fonction exponentielle.
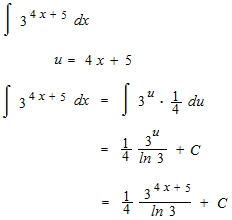
Le calcul de la valeur de nombre népérien.
lorsque x = 1, la limite de taux moyen de variation, soit la pente de la tangente est 1.
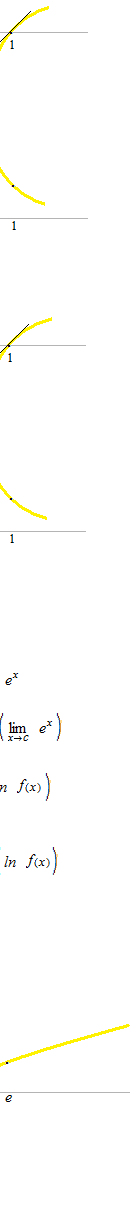
L’inclinaison de la ligne tangente est 1.
La valeur du nombre e ne peut pas être calcule d’un seul coup d’une équation.
n = 100 2.704814
n = 10 000 2.718146
n = 100 000 2.718268237
e = 2.718281828…….
Si vous utilisez calculatrice de Windows, vous aurez ce nombre népérien pour fonction exponentielle, fonction logarithme naturel,etc.comme ceci.
1
Inv
ln
=
2,7182818284590452353602874713527
Par exemple pour EXP(3) ou e3
e3=20,085536923187667740928529654582
3
Inv
ln
=
20,085536923187667740928529654582
sinon
1
Inv
ln
x^y
3
=
20,085536923187667740928529654582
Il y a un bouton EXP. Il est justement pour faire glisser le point flottant. Ce bouton EXP ne fonctionne que dans le système décimal.
0.88888888
EXP
3
=
888.88888
La probabilité de tout rater.
On lance un dé en essayant de faire sortir numéro 1 . Si l’on le lance 6 fois, la probabilité d’avoir une fois 1 est à 100%.
La probabilité de n’avoir aucune fois 1 , la probabilité de tout rater, c’est-à-dire, la probabilité d’avoir 6 fois un des autres cinq points est de 33.5%.
Si l’on fait un autre jeu de tirage qui a une basse probabilité, par exemple une fois sur 60 , la probabilité de n’avoir pas une fois le numéro qu’on attend est de 36.5%.
Un autre jeu de tirage qui est encore difficile. Une fois sur n. On tire n fois pour avoir 100% de probabilité, mais il a quand même e-1 de probabilité de tout rater.
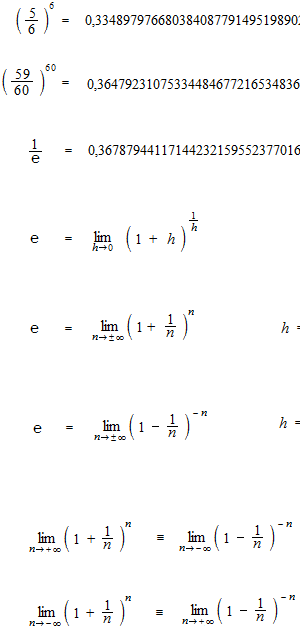
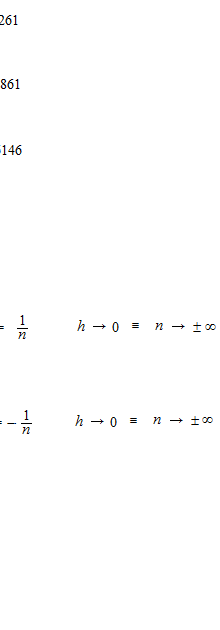
n est le nombre qui fait augmenter le nombre de partition, on prend l’infinie positive.
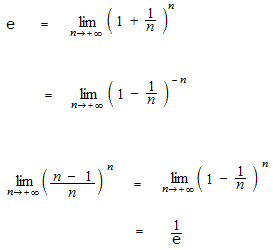
La définition de la fonction exponentielle, utilisant la limite.