Riemann sum
Rectangle method → Riemann sum → definite integral
Find area under courbe of positive and continuous function on the interval [ a , b ] .
Riemann sum transformed rectangle method into definite integral.
Rectangle method
Rectangle method must have been used from ancient times. For graphic curves, aire is the sum of strips of equal width.
Riemann sum
Riemann sum is a kind of rectangle method. As Riemann sum is supposed to going to be treated with limite operation, the choice of the height in each rectangle strip is omitted.
For differentiation, point of Lagrange’s mean value survives limit operation and represents the slope as parameter for the variable of derivative.
As for integration by Reamann sum, any point can represent the points in the width of each rectangle strip. The point of the mean value theorem for integration is that point, but it is not necessary to have mean value.
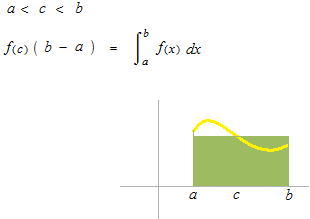
There must be such a point c .
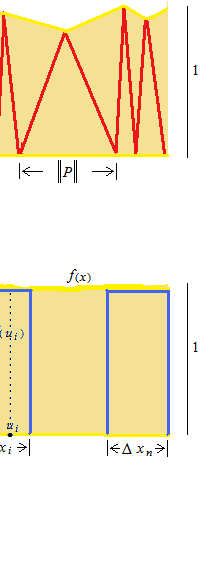
In Reamann sum, bande widths are not necessarily equal. A width ab can not be devided by infinity.
It looks paradoxal to make the largest width ||P|| infinitely small. So it should be said, epsilon delta like, that however small the largest width is.
Definite integral.
Limit of Riemann sum. It is called also Riemann integral.
Rectangle method
Rectangle method must have been used from ancient times.
Method of rectangles is easy to understand except the sense of sigma.
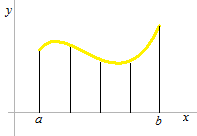
We divide [ a , b ] into n equal subintervals. The width of each subinterval is Δx.
b = a + n (Δx)
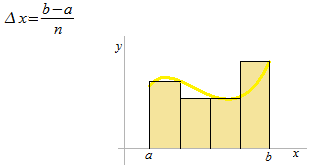
The height of each rectangle is always right side.
If there is someone who chooses left side and from i = 0 to n − 1 , that person must be crazy.
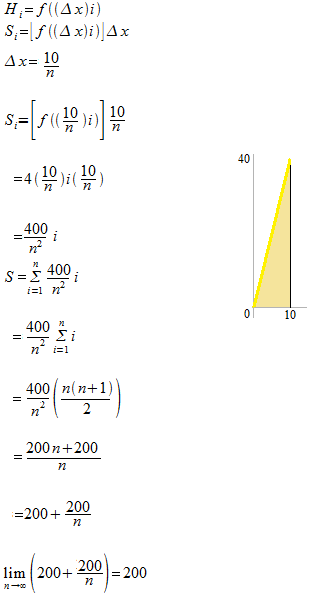
Height H of the i th rectangle
![]()
Area of the ithrectangle.
![]()
The sum of all rectangles S
![]()
Area A
![]()
Find the area.
y = 4 x
[ 0 , 10]
y = − x2 +16
[ 0 , 4 ]
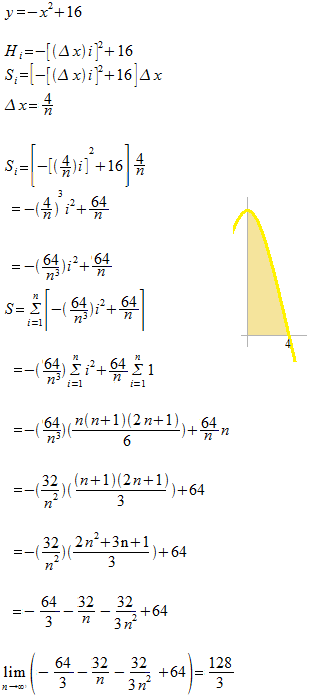
Area of a semicircle
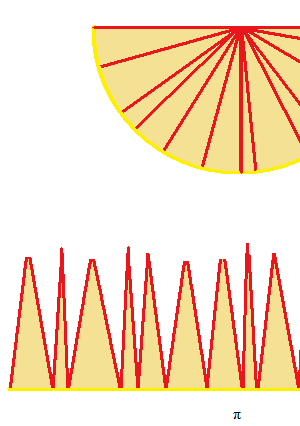
The figure seems to be divided into many isosceles triangles, but in fact, they are small circular sectors. The base line is not a straight line. The heights of these sectors are not equal.
Let Pis the broadest interval. The value of the length of P is represented by ||P||.
The equal division would be easier at this point. But, after, when you divide the semicircle into infinitely small pieces, you can not divide into equal intervals. Because infinity is not a number, but only an expression. You can not divide a number by infinity to get equal intervals. You can not divide anything by an infinite number. So, instead of that, we say “whatever the size of the largest interval”, that means “always”. Because ” very small” is an ambiguous adjective.
The calculation of the area of each circular sector is not possible, in stead, we link all vertices. This line is extremely complex but it is a function. We name it f(x) .
Differentiate means find the direction of a point.
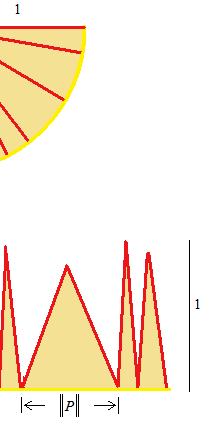
Now, the width of each interval is infinitely small. The horizontal lines are nearly straight. All heights converge to 1. A collection of infinitely thin isosceles triangles.
That makes almost a big rectangle. We now consider this big rectangle as a collection of very thin rectangles. In the figure below, three rectangles are very large to show better.
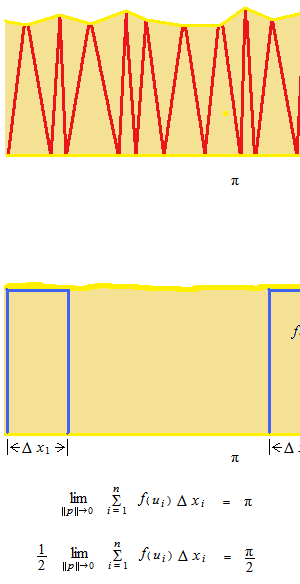
These equations read …
As the largest interval is infinitely close to 0 , or whatever the largeur of the largest interval ||P||, the total of the big rectangle should be π.
Where …
n is the number of the very thin rectangles.
Δ x is the width of each interval.
Any x value within each interval is called u.
The height of each rectangle is f (u)
Δ x , u , f (u)of the i threctangle are Δ xi , ui , f (ui)
And the area of a semicircle is π divided by 2.
Riemann sum
Riemann sum is a kind of rectangles method. But Riemann sum is presupposed that it will be calculated with limit. The Riemann sum is therefore deprived of the things that are not compatible with limite operation.
Since the Riemann sum will be calculated with limit, the choice of height has no place to discuss. Width of rectangles will be infinitely small, so there will be no questions of the choice of height.
As all rectangles will have infinitely small width, in the Riemann sum, equality of width is excluded.
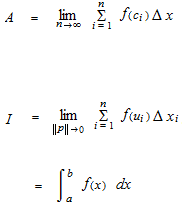
A is the formula of the method of rectangles.
I is the formula for the Riemann sum with the limit, therefore definite integral that is to say, the Riemann integral.
||p|| is the width of the largest rectangle.
Definite integral is the limit of Riemann sum.
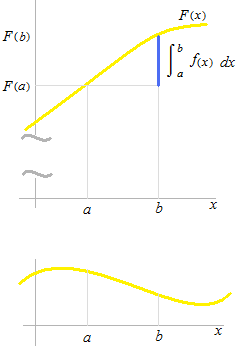
Area under the curve of f(x). [ a , b ]
That is also the difference between F(a)and F(b)
If we assume that dx,dt and dyas length values, we can imagine integration in another way.
It can be said that dx, which is denominator of proportion, is restored to Δx, which is a length value.
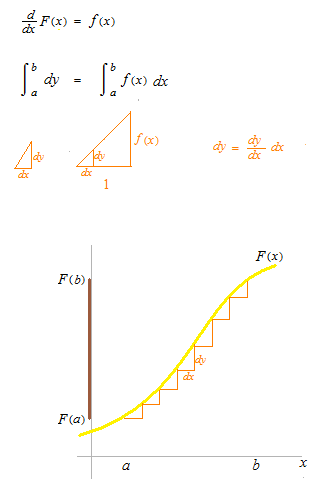
The result of an integration is a number.
An integral is a number.
There is no function F(x) as a result of an integration of f(x). [ a , b ] .
Instead, there can be a function I(x) as the function of de difference between F(a) and F(x)
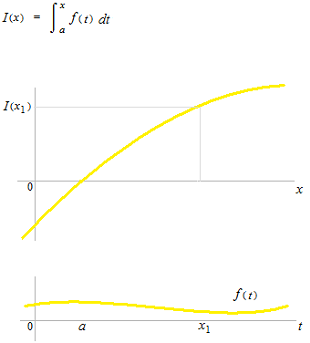
This way of integration is used to get natural logarithm function.
y = ln x from y = 1/x
