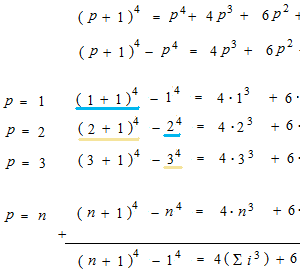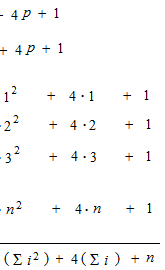Sigma
La notation sigma pour intégration définie
Le rôle de la notation sigma, c’est de faire une expression avec ‘ n ‘ en utilisant une
expression avec ‘ i ‘.Il s’agit de l’effacement des indices ‘ i ‘ dans une sommation.
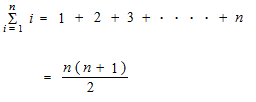
La sommation doit commencer par i= 1. Ne mettez pas i= 0 à moins d’un cas très très spécial.
La sommation se fait jusqu’à n. Ne mettez jamais un nombre sinon la notation sigma perdra le sens.
Le but du sigma est d’effacer ‘ i ‘, donc le deuxième terme, troisième terme, … sont inutils.
Voici comment écrire le sigma dans les maths.
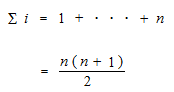
Depuis des milliers d’années, nous, les hommes, avons cette forme de comptage n(n+1)/2. Cette forme de fraction s’appelle sigma i. Sigma i s’écrit avec n . i est déjà disparu.
![]()
Les hommes de caverne auraient trouvé une autre fraction. C’est le sigma i2
![]()
L’expression de terme général avec l’indice i sera changée en une expression de la somme avec le dernier indice n. En prenant l’infinité, n de 1/n , lui aussi, disparaîtra. Et on aura la valeur de l’intégrale définie.
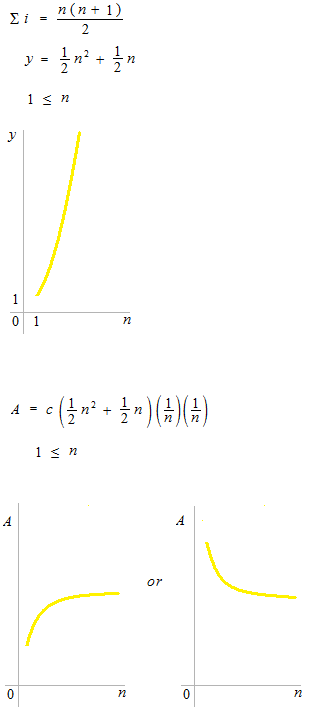
Intuitivement, le sigma peut être imaginé comme quelque chose qui est en forme de triangle ou pyramide et si l’on fait une multiplication avec un nombre, on aura la somme. Pour une fonction à puissance m, la courbe de sigma im est infiniment montante. Multipliant par hauteur (1/n)m 、et par largeur (1/n), fonction de l’aire converge à une valeur définie.
La simplicité de l’addition dans le terme général promet la possibilité de calcul d’aire.
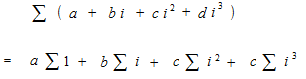
Comme les hommes de caverle, on va conpter des cailloux.
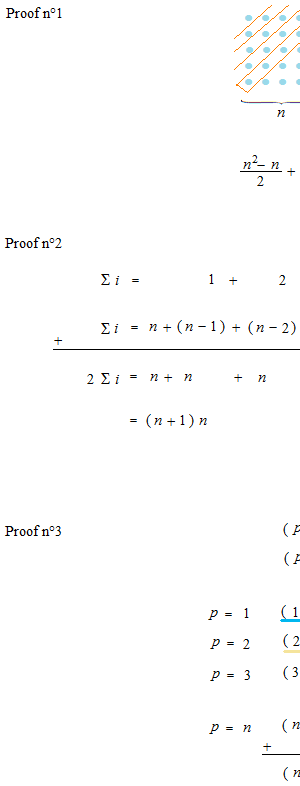
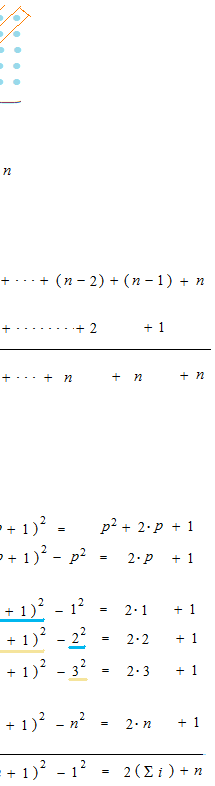
Cette méthode peut être utiliée pour i à plus haute puissance.
![]()
On n’est pas toujours obligé de compter le nombre au moyen de diagramme, mais le volume de pyramide rend le dénombrement possible. On considère les solides comme un empilement des cailloux. Pour compter des cailloux en un pyramide, avant de diviser le prisme triangulaire par 3, il faut ôter la face commune et diviser et on l’ajoute.
Il s’agit de compter le nombre de cailloux de ce pyramide qu’on divise en deux.

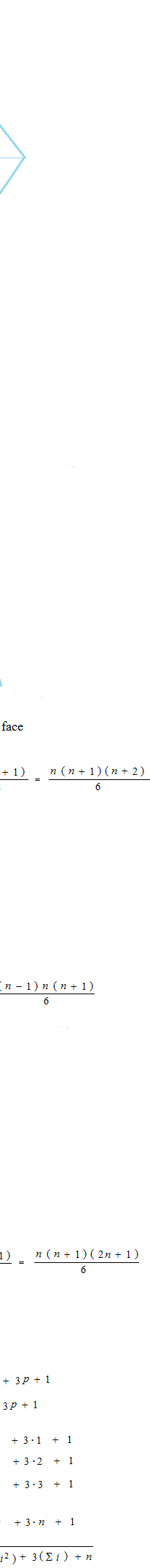
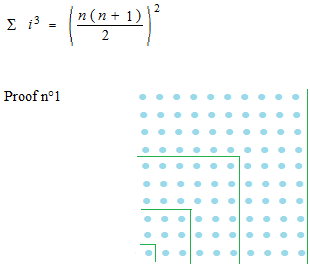
Si l’on essaie de compter, ce sera en quatre dimensions. En deux dimensions, cela doit être comme ceci.
Proof n° 2
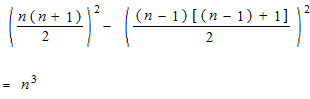
On pourrait tricher comme ça.
Proof n° 3