逆関数の導関数
y = x を恒等関数と呼びます。
恒等関数 y = x をふたつの関数の合成関数とみなすと、 y = x を構成する対の逆関数の組み合わせは無数にあります。
合成関数 逆関数

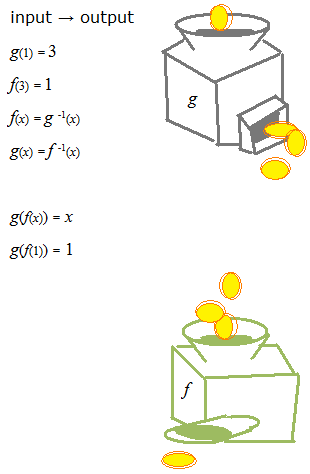
お金を入れると3倍になって出てくる機械。1€ を入れると3€ 出てきます。その逆は、お金が3分の1 になって出てくる機械ということになります。ふたつの機械を組み合わせると結局1€ は1€ になります。
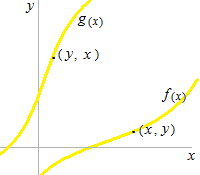
f(x)上に (x, y)という点があると必ずg(x)上に (y, x)という点があるので, グラフは恒等関数 y = xに関して対称になります。
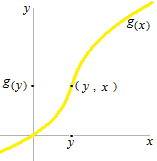
逆関数を語るとき、しばしば xと y の文字が変数名(軸名)と変数の一時的な値として混用されます。点 (y , x) とは、或る点(x, y)の xの値が yの値、yの値が xということ。ここでは g(y) とは、或る関数 g(x) の xの値が yということです。
稀に積分で縦軸のほうを独立変数にとることがありますが、逆関数を云々するときは通常、括弧の中の変数は横軸の値です。
(x, y) ではなく (a, b) あるいは (y1 , x1) あるいは (u1 , x1) としたほうが明確になるのですが、関数として云々しているので括弧の中は定数ではなく変数を書きます。g(y) の y は f (x) の答です。
g(x) は f (x) の逆関数。なぜかというと、 g(y) = xだからです。
g(x) の xは変数名(軸名)。
g(y) の yは変数 xの一時的な値のすべて。
もしも g(y) = xならば g(x) は f(x) の逆関数になります。
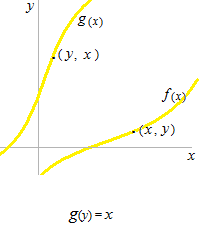
逆関数は1対1で対応していなくてはなりません。
逆関数の導関数
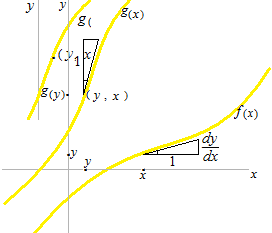
逆関数の導関数
逆関数のグラフは y = xの線に於いて対称なので、導関数の直角三角形も対称になっています。
ふたつの逆関数を組み合わせた合成関数の微分は1 になります。
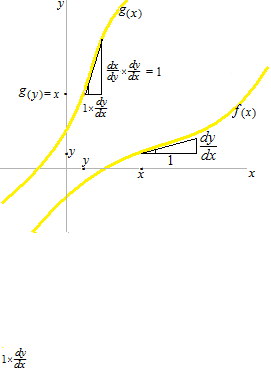
と書いてあるのは、dyの ∞ 倍 としての 1 は dxの ∞ 倍としての 1 と目盛りが違うからです。座標がふたつあると考えるべきでしょう。
但し、 ∞ は数ではないので ∞ 倍 という言い方は正しくありません。
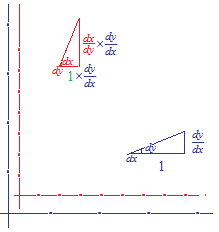
チェーンルールを使います。
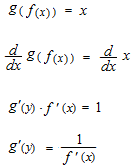
直角の式とはちがいます。
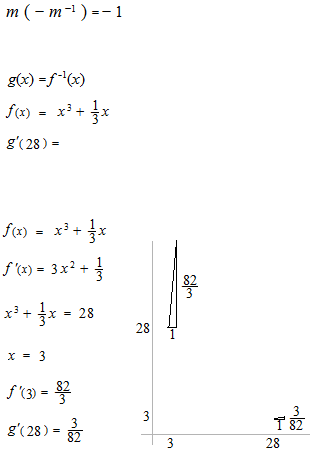
暗算で解けます。
