チェーンルール 合成関数 微分
合成関数の用途
1. 因数分解。
2. 微分に於けるチェーンルール。公式に当てはめるため。
3. 積分に於ける置換。公式に当てはめるため
4. 自然対数関数と指数関数の関係が逆関数の関係であるということ。
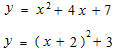
普通の方程式で括弧の中を先に計算するという順序も既に合成関数といえます。式が簡単になりますが、微分積分の計算に於いては外側の式の変数の目盛りの幅が変わります。
分配法則、結合法則、交換法則 などによって計算の順序による違いがでます。
入れたお金が3倍になる機械があったとします。その機械に g と名前をつけます。
もうひとつ機械 h があり、その機械はお金を2倍にします。
g から出てきたお金をそのまま h に入れると何倍になるでしょうか。
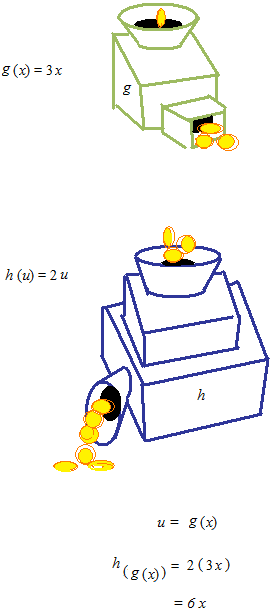
チェーンルールは下の図から想像できます。
チェーンルール, Chain rule, で合成関数の微分をします。
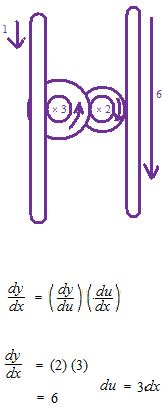
直方体の体積で高さを変数にするとこのようになります。
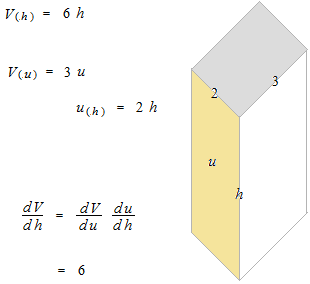
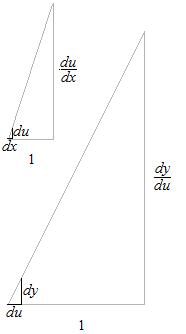
直方体の体積で高さを変数にするとこのようになります。
この二つの大きな三角形はそれぞれ独立しています。
tangentは横1に対する縦の割合を意味します・
それぞれの1の長さが違っています。
二つの関数 g(x)と h(u)では目盛りの大きさが変わると考えることができます。
合成関数とは或るひとつの複雑な関数をふたつ以上の単純な関数の組合せに変えるということです。
まず最初に一つの関数があり、それを二つの関数の組合せにした場合、全部で三つの関数があるということになります。
外側の関数はそれ自体で独立しているので、内側の関数が外側の関数の一部となっているわけではありません。
以下、ふたつの関数のみの組合せで合成関数の微分を考えます。内側の関数が外側の関数のグラフの座標の目盛りを決めているともいえます。
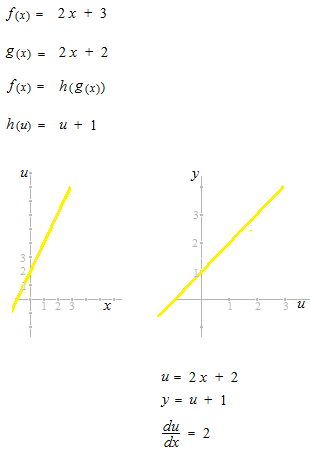
上のようなグラフにしてみました。
du は dx の2倍なのでふたつの座標の目盛りの単位「1」の長さも2倍にしました
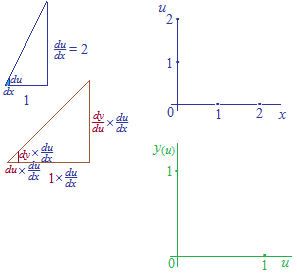
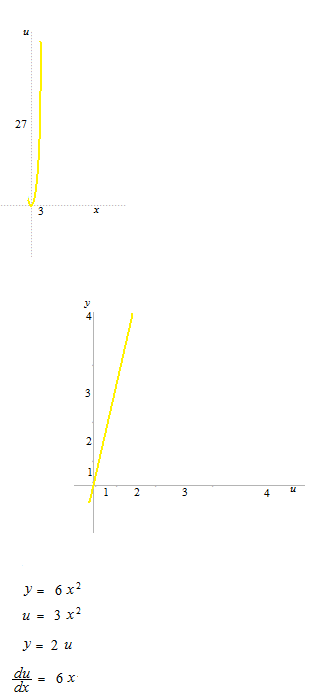
u が一次以外になると、u – yの座標は伸び縮みします。
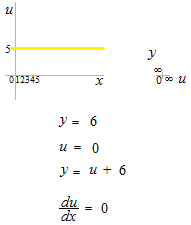
定関数を合成関数にしてチェーンルールをしようとすると、分母が du = 0になってしまいます。
チェーンルール、またはチェインルール
