二階微分
導関数をさらにもう一度微分することを2階微分と呼びます。
微分積分は電気の計算などにも使われますが、私たちの直感的な把握ということではつぎのような関係が想像しやすいようです。
半径を変数にとった球の体積、表面積の関係
円の面積、円周の関係
時間を変数にとった距離、速度、加速度の関係など。
距離の導関数が速度、速度の導関数が加速度になります。
二つに分けて考えれば分かりやすいですが、距離と時間を見て、いきなり加速度を思い浮かべるのは難しいはずです。
2階微分はこのように書きますが、なぜでしょうか。
![]()
微分は dyの dxに対する比率ですから、dyを dxで割ったものです。できた関数が導関数 y’ です。三角関数の tanと同じです。
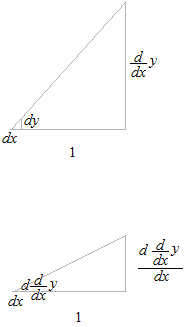
その y’ を微分すると2階微分 y” です。
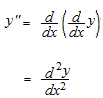
dx2は (dx)2を意味します。
d^2y/dx^2 なぜ2階微分はこのように書くのか
