103 Lagrange, Mean value theorem
Lagrange’s Mean value theorem
Lagrange’s Mean value theorem looks too much obvious, but very important. Mean value theorem can prove that, for example, when a derivative is positive, its antiderivative is increasing.
If f'(x) > 0 throughout [ a, b ], show that f(x) is always increasing.
x1 , x2 : Any two numbres in [ a, b ]
x1 < x2
( x2– x1 ) f'(c) = f(x2) – f(x1 )
Lagrange’s Mean value theorem
( x2 – x1 ) > 0
f'(c) > 0
Then
f(x2) -f(x1)> 0
Mean value theorem is based on Roll’s theorem.
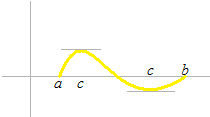
Roll’s theorem
If
a < b
g(a) = g(b)
then there must be at least one element c such that
a ≤ c ≤ b
g'(c) =0
Mean value theorem
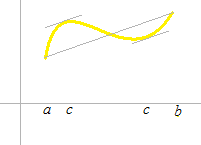
There must be at least one element c such that
x1 ≤ c ≤ x2
![]()
First, let’s take a look at linear functions.
f(x) and g(x) are linear functions.
Express g(x) with f(x) .
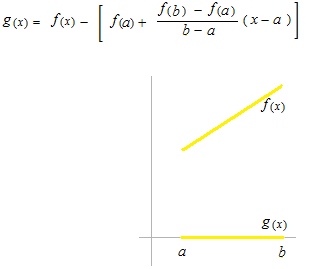
This time, f(x) is not necessarily a linear function. But the same equation works.
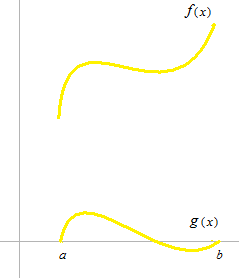
Now we define withf(x) a function g(x) which is model type of Roll’s theorem.
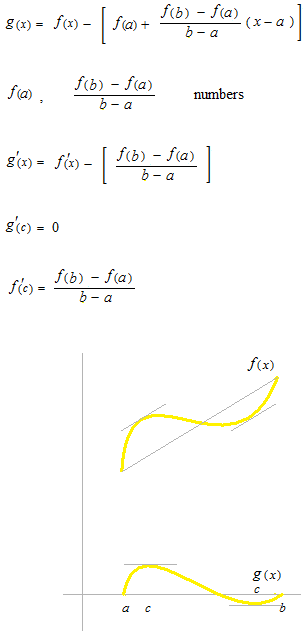
If f ”(x)> 0 throughout [ a , b] , let’s see that f(x) is always concave up.
First of all, write the equation of the tangent line at the point ( p , f (p)) on f(x).

y = f(p) + f ‘(p) ( x – p )
We use mean value theorem again.
p< c < x
What kind of c must be there?
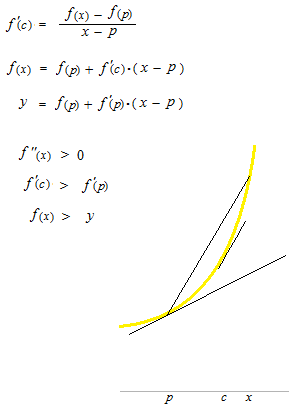
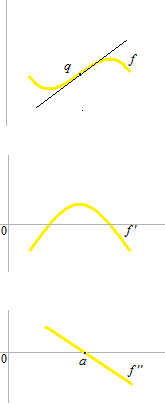
As the point q in this figure, a point where a curve change its concavity is called inflection point. The tangent line at point q on this graph.
( y − f(a) ) =f'(a) ( x − a)
Lagrange’s Mean value theorem
