Lagrange, Théorème des accroissements finis
Le théorème des accroissements finis peut sembler trop évident parce que c’est un théorème, mais très important. Il sert à démonter, par exemple, le fait que quand la dérivée est positive, la pente de sa primitive est montante.
Pour f'(x) > 0 sur [ a, b] , démontrons que la courbe de f(x) est toujours montante.
x1 , x2 : deux nombre dans [ a, b ]
x1 < x2
( x2 – x1 ) f'(c) = f(x2) – f(x1 )
Théorème des accroissements finis,
( x2 – x1 ) > 0
f'(c) > 0
donc
f(x2) – f(x1) > 0
Le théorème des accroissements finis est basé sur le théorème de Roll.
Théorème de Rolle
Si
a < b
g(a) = g(b)
alors il existe au moins un élément c tel que
a ≤ c ≤ b
g'(c) =0
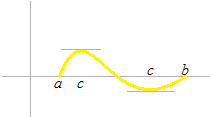
Théorème des accroissements finis
alors il existe au moins un élément c tel que
x1 ≤ c ≤ x2
![]()
Pour commencer, nous prenons des fonctions affines.
f(x) et g(x) sont des fonctions affines.
Exprimez g(x)avec f(x) .
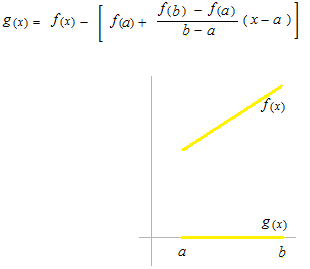
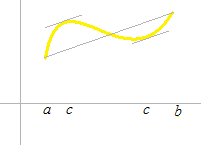
Cette foix, f(x) n’est pas nécessairement une fonction affine. Mais la même équation marchera.
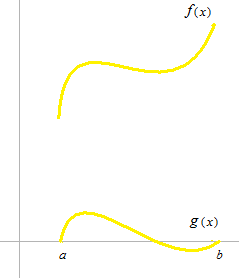
Nous allons définir à partir def(x) une fonction g(x) , qui est typique pour théorème de Rolle.
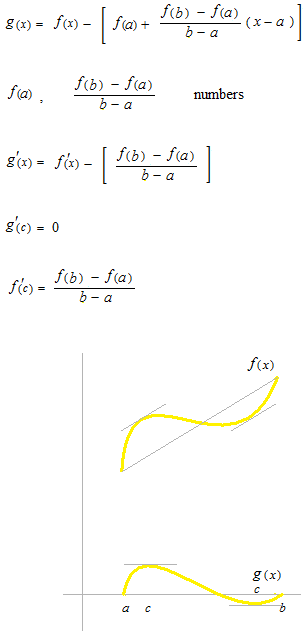
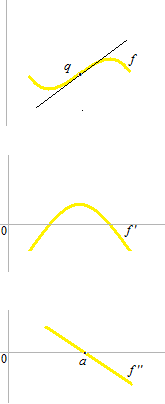
f ”(x)> 0 sur [ a , b] , nous allons démontrer que le graphique de f(x) tourne sa concavité vers les y positifs.
Nous utilisons encore une fois le théorème des accroissements finis.
p< c < x
Quelle sorte de c doit-il y avoir?

Tout d’abord, écrivez l’équation de la tangente au point ( p , f (p)) sur f(x) .
y = f(p) + f ‘(p) ( x – p)
Nous utilisons encore une fois le théorème des accroissements finis.
p< c < x
Quelle sorte de c doit-il y avoir?
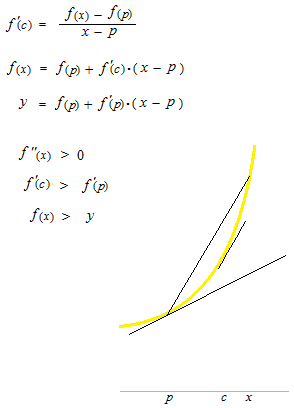
Comme le point q de la figure, le point où change la concavité d’une courbe s’appelle point d’inflection. La tangente au point q sur ce graphique est
( y − f(a) ) =f'(a) ( x − a)