Limit
This function is not continuous on [a , b] .
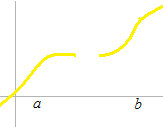
Continuity at a point. That is the function converges at that point as a limit. Any point belongs to the series that goes toward that point. Continuity does not mean that numbers are sticking together.
The function must be continuous on [a, b]
The function must be continuous to the ends.
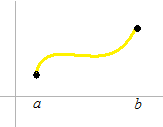
The function is not differentiable at p . The slope is not same on both side of p .
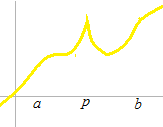
In order to differentiate, the function must be differetiable on ( a , b)
The two ends can’t be defined concerning thier further behavior.
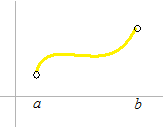
In the pages of this site, the words “differentiable on ( a, b) and continuous on [ a, b] ” are almost always omitted. If you go in for examination, don’t forget to mention it. Definition of domain is always required, especialy in order to avoid the denominator of a fraction being 0.
Limit
Why limit is necessary ?
When we determine derivative of a function, why limit is necessary? Why even for a constant function or for a linear function the limit is essential to derivation?
The reason why a limit operation is necessay even for a constant function and also for a linear function.
But, of course, real continuity of function is out of question. Between a number and another number next to it, there are infinitely many numbers. A number never sticks to a next number. Calculus is based on the fact that true continuity can not be discussed.
Continuity about a number is the convergence of the series around that number.
When an operation of limit about a point of a function has a definite answer, that part is said converging to that value. The series of the function is brought at bay on that value. When a function is easy enough, its convergence might be clear, but not always. As limit is a very important step for differentiation and integration, intuitive way of solving limit operation is not enough foy the theoretical understanding.
Limit operatiion can be done by normal method or by l’Hôpital’s rule. l’Hôpital’s rule will be explained later in this site. That is a very easy way to get the limit answer when you have an expression in frantion form of which both numerator and denominator are infinite, form ∞/∞ or form 0/0. You just only do differentiation separately numerator and denominator.
The concept of limit is needed to make a derivative to determine the slope of tangent line of a curve by differentiation and to determine the area under the curve by definite integral.
A derivative is a function. It gives one yfor one x.
f'(x1)
Rate of change is determinated by the difference of y between two values of x.
![]()
After narrowing Δxbetweenx1 and x2 , we have the value for only one x. Thatx will be used as parameter of the derivative function.
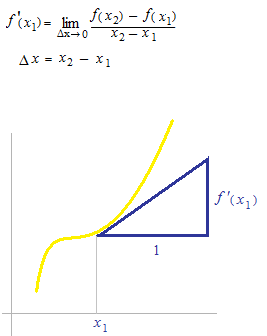
Often derivative is considered to be the rate of chage between two points. But a derivative is what we have after an limit operation, therefore it doesn’t concern with two points any more.
It can be said only as the slope of the tangent line at one point.
When you do a limit operation, narrowing an interval between two points to the extreme, the point which will survive is the point c of the Lagrange’s mean value theorem. Average between two points will become value on one point. That will used as input parameter of the function derivative.
The mean value theorem of Lagrange is the back bone of calculus.
