Limite
Cette fonction n’est pas continue sur [ a , b] .
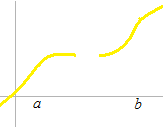
La continuité sur un point, c’est que la fonction converge à ce point comme une limite. N’importe quel point appartient à la série qui va vers ce point. La continuité ne signifie pas que les nombres soient collés les uns avec les autres.
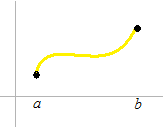
Une fonction est continue sur [ a , b] . La fonction est continue jusqu’aux bouts.
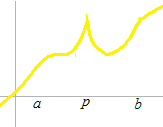
La fonction n’est pas différentiable àp . L’inclinaison est différente à deux côtés de p.
Une fonction est dérivable sur (a , b).
Les bouts ne peuvent pas être définis de leur accroissement.
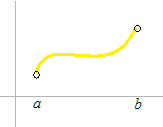
Ces mots “( a , b) dérivable et [ a , b ] continue ” sont presque toujours omis dans les pages de ce site, mais n’oubliez pas de les noter s’il s’agit d’un examen. La description du domaine de x est obligatoire, surtout quand le démoninateur d’une fraction pourrait être de 0.
Limite
Pour déterminer la dérivée d’une fonction, pourquoi l’idée de la limite est-elle nécessaire?
Même pour une fonction constante ou pour une fonction affine, pourquoi l’idée de la limite est nécessaire pour la différentiation?
Lorsque une expression de la limite a une valeur définie, cette expression est dite convergente.
Quand l’expression est assez simple, la convergence est évidente. Mais, ce n’est pas toujours le cas. La méthode intuitive n’est pas suffisante pour la diversité des fonctions.
Déterminer la limite avec opération normale, ou bien la régle de l’Hôpital facilite parfois la détermination. La régle de l’Hôspital sera éxpliquée plus tard dans ce site avec la compréhension intuitive.
L’idée de la limite est utilisée quand nous déterminons l’inclinaison de la ligne tangente d’une courbe par une différentiation et l’aire sous une courbe par intégrale définie.
La dérivée est une fonction, elle détermine un ypour un x.
f ‘(x1)= y1
Or, le taux d’accroissement est déterminé par changement de valeur de y entre deux valeurs d’x .
![]()
Δx rétréci entre x1et x2, on aura une seule valeur d’ x.
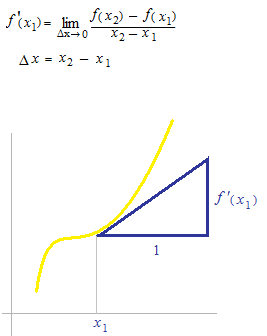
On dit très souvant que la dérivée est l’inclinaison entre deux points à très petit écart, le taux d’accroissement entre deux valeurs d’x.
Mais, comme la dérivée est une fonction que nous obtenons après une opération de la limite, cela ne concerne plus la diférence entre deux points ni “voisinage” d’un point.
La dérivée est une fonction, elle aura un y contre un x. Un seul x sera utilisé comme paramètre.
La dérivée ne peut être exprimée que comme l’inclinaison de ligne tangente à un point.
C’est le point c du théorème des accroissements finis de Lagrange qui restera dans l’ultime restriction de la limite. Pour le calcul différentiel, le point c du théorème des accroissements finis de Lagrange change la valeur de la moyenne entre deux points en une valeur sur un point. Ce sont la valeur de la dérivée et la input valeur, paramètre, pour la variable de cette fonction dérivée. Donc l’idée de la limite est nécessaire même pour une fonction constante et pour une fonction affine.
Le point du théorème des accroissements finis de Lagrange est la colonne vertébrale de la différentiation.
