Volume du tétraèdre
Dérivée des figures géométriques
Quand l’axe horizontal prend la valeur du temps comme sa variable, il s’agit souvent d’une fonction qui exprime un changement de la vitesse de quelque chose. La dérivée de cette fonction sera la fonction qui exprime la grangeur de ce changement même.
Si c’est une courbe qui exprime la distance parcourue d’une voiture, la dérivée de cette fonction sera la courbe qui exprime la vitesse de cette voiture.
S’il s’agit d’un solide, l’axe horizontal ne prendra pas le temps, mais la longueur comme la variable. La dérivée de cette fonction sera la fonction qui exprimera la grandeur du changement de volume au fur et à mesure de cette longueur.
Soit une fonction qui exprime le volume d’une pyramide ou d’un cône, dont la variable prend la hauteur, la dérivée de cette fonction pourra exprimer l’aire de la base.
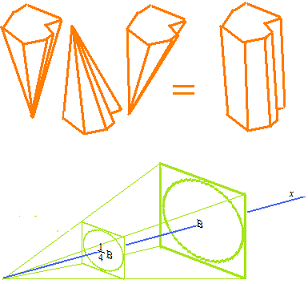
Le volume d’une pyramide ou d’un cône est de 1/3 du volume d’un prisme ou d’un cylindre à la même base.
0 ≤ x variable : hauteur d’une pyramide ou d’un cône
B constante : l’aire de la base quand x = 1
Bx2 l’aire de la base
f’ =Bx2 la limite de la moyenne de taux d’accroissement du volume
volume de pyramide ou de cône.
![]()
Bx3 Volume de prisme ou de cylindre
De même que la dérivée de l’aire de cercle est égale à la circonférence, en mettant la variable x comme la longueur du rayon, pour que la dérivée d’un carré soit égal à la somme de quatre côtés, comment la variable x doit-elle être mise?
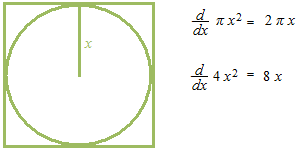
Quand nous mettons x comme le rayon du cercle inscrit, la dérivée de l’aire de carré sera égale au total des côtés.
Essayons, maintenant, avec un triangle équilatéral en prenant le rayon du cercle inscrit comme x.
Est-ce que la limite de la moyenne de taux d’accroissement est égal à la somme de la longueur des trois côtés?
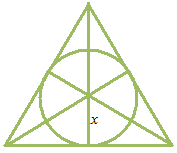
x comme le rayon du cercle inscrit
Longueur d’un côté est de
![]()
l’aire de triangle équilatéral
![]()
La dérivée de volume dune sphère est égale à la valeur de superficie.
![]()
Nous allons essayer avec un cube.
x comme le rayon du cercle inscrit
La longueur d’un côté.
2 x
Le volume du cube.
8 x3
Superficie de cube
24 x2
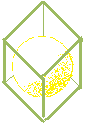
Pour finir, on va essayer avec un tétraèdre.
x comme le rayon du cercle inscrit
a est la longueur d’un côté de tétraèdre.
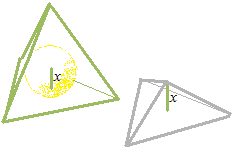
Si l’on divise le tétraèdre en quatre petits pyramides triangulaires dont la base est une des quatre faces du tétraèdre, la hauteur du petit pyramide sera x.
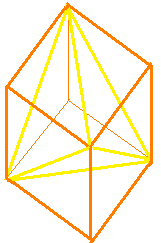
Nous allons utiliser le fait que si nous relions quatre coins d’un cube, nous aurons un tétraèdre dedans.
C’est-à-dire, nous pouvons construire un grand cube avec un tétraèdre et
quatre pyramides triangulaires appropriés à l’extérieur.
Longueur d’un côté de ce grand cube.
![]()
Le volume chacun des pyramides triangulaires qui sont autour du tétraèdre.
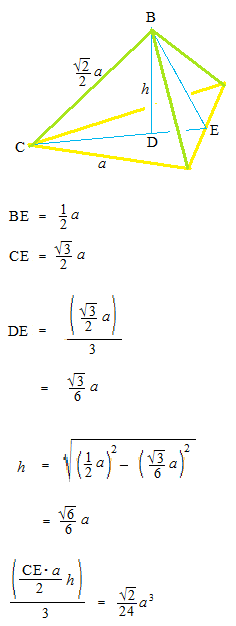
Volume de tétraèdre
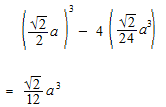
Le volume de chacun de quatre petits pyramides.
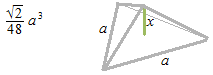
L’aire de la base des petits pyramides triangulaires.
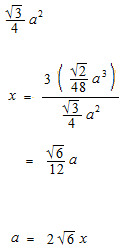
Le volume du tétraèdre.
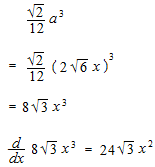
La superficie du tétraèdre.
![]()
x comme le rayon du cercle inscrit.
