Limit of average rate of change, Tangent
When the problem is about something changing its state, very often, the horizontal axis takes the time as its variable.
A car ran for 2 hours and traveled 160km. The average speed was 80km / h.
Usain Bolt ran 9.58 seconds on the 100m track. The average speed was 37.78km / h.
The average speed equals distance divided by time.
He ran for 0.00266hour and moved 0.1km.
The calculation is done with two point: departure and arrival.
Therefore the result must be an average.
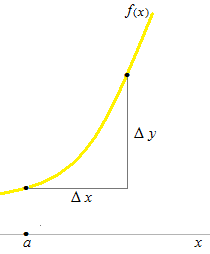
“Δ” means the difference between two values.
Δxas time between start and finish.
Δy as distance between the starting position, f (a) and the arrivalf(a+ Δx).
So average, that means that two points, the departure point and the arrival point are separated. Only these two points represent the entire period. What happened between these points is ignored. That is average.
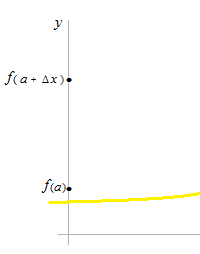
average: A km/h
![]()
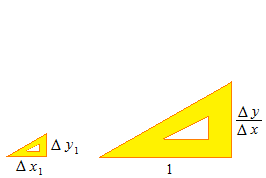
In calculus, the trigonometric functions take arc length for the variable.
As for straight line, its slope is not expressed by degrees but by the proportion of Δx and Δy. This proportion is the tangent.
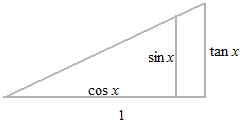
Tangent expresses proportion of two values of any sort in a length value.
Tangent is average of Δy by Δx . The average rate of change is expressed by tangent.
An area is a volume with height 1 .
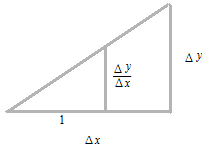
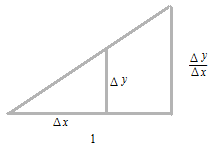
Differentiation is a calculation of the slope of a tangent line. A tangent line touches the curve at one point, as narrowing Δx infinitely.
Differential coefficient is the slope at a point.
Derivative is the function which expresses all the differential coefficients of a function.
Numerator and denominator of the fraction of proportion are indicated by dyand dxrespectively.
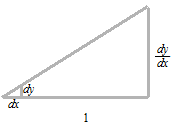
dy and dxare used always together, as they are the numerator and the denominator of a fraction.
Δxis a length value and dx is the denominator of a proportion.
In a differentiation, Δx is used as if it were dx.
In a integration, dxis used as if it were Δx.
