Limite de la moyenne de taux d’accroissement, Tangente
Quand il s’agit d’un problème concernant quelque chose qui change de son état, très souvent, l’axe horizontal prend le temps comme variable. À partir de quel moment et jusqu’à quel moment, ce changement se passe.
Une voiture a roulé pendant 2 heures et elle s’est déplacée de 160 km. La vitesse moyenne est de 80 km/h.
Usain Bolt a couru pendant 9,58 secondes et il s’est déplacé de 100 m. La vitesse moyenne est de 37,78 km/h.
La vitesse moyenne est égale à la distance divisée par le temps.
Il a couru pendant 0,00266 heure et il s’est déplacé de 0,1 km.
Le calcul se fait des données des deux points: le départ et l’arrivée.
Par conséquent le résulta sera une valeur de la moyenne.
‘ Δ ‘signifie la différence entre deux valeurs.
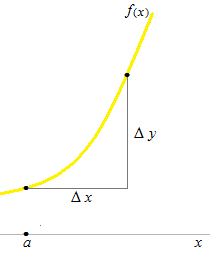
Δxest la durée entre le départ et l’arrivée.
Δyest la distance entre le départ, f(a) et l’arrivée, f(a+ Δx ).
Donc, la moyenne, cela veut dire que les deux points, le piont de départ et le point d’arrivée sont distincts. Ils sont séparés. Cest seulement les valeurs de deux bouts qui représentent tout ce qui se passe dans la période. Ce qui s’est passé entre ces bouts sera ignoré. Donc, c’est la moyenne.
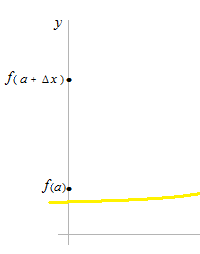
la moyenne: A km/h
![]()
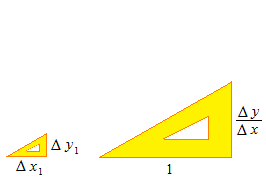
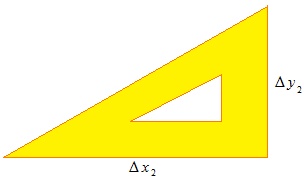
Dans le cancul différentiel, les fonctions trigonométriques prennent la longueur d’arc pour leur variable.
En ce qui concerne la ligne droite, son inclinaison ne sera pas exprimée par l’angle en degrés, mais par la proportion de Δy à Δx . Cette proportion est la tangente.
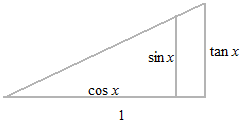
La tangente exprime la proportion de deux valeurs en une longueur.
La tangente est la moyenne de Δy sur Δx . La moyenne de taux d’accroissement est exprimée par la tangente.
L’aire est le volume à hauteur 1 .
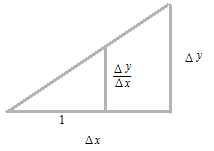
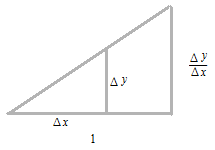
La différentiation, c’est le calcul pour avoir la valeur de l’inclinaison de la ligne tangente, qui touche la courbe à un point, en rétrécissant Δx à infiniment petit. La fonction qui est le résultat de la différentiation s’appelle dérivée.
Le numérateur et le démominateur de la fraction de cette proportion sont respectivement dyet dx .
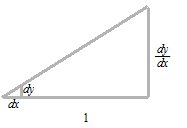
dyet dx sont utilisés toujours ensemble, comme ils sont le numérateur et le démominateur d’une fraction.
Δx est la valeur de longueur et dxest le démoninateur de proportion.
Dans une différentiation, Δxest utilisé comme si c’était dx.
Dans une intégration, dxest utilisé comme si c’était Δx.
