044 Circonferenza trigonometrica


“Ieri, ho composto una canzone.”
“Com’è la melodia?”
“Per esempio, la quinta croma della terza battuta è un mi bemolle.”
Le funzioni trigonometriche e la circonferenza trigonometrica.
La curva della funzione seno è una bella curva, che ha la pendenza di 45 gradi, la lunghezza di π e l’area di 2. L’ammirazione per la bellezza di questa curva potrebbe essere la base della comprensione delle funzioni trigonometriche. Da una parte, la forma della curva della funzione seno è molto utile per il calcolo differenziale e integrale, d’altra parte, la circonferenza trigonometrica è solo una figura che mostra visivamente la definizione della funzione seno, e questa figura è altrimenti inutile.
La circonferenza trigonometrica non è la funzione seno. La circonferenza trigonometrica dà illusioni che la circonferenza trigonometrica mostra le funzioni trigonometriche, che la funzione seno e la funzione coseno sono il movimento circolare del punto P sul cerchio, e che la funzione seno e la funzione coseno sono geometricamente considerate nel secondo, il terzo e il quarto quadrante. Una volta la curva della funzione seno è stata fatta, il calcolo non necessita più la circonferenza trigonometrica.
Mentre ci sono sei funzioni trigonometriche, la cotangente, la secante e la cosecante sono semplificazioni del seno o del coseno, che sono sotto la forme di frazione. Queste sono semplificazioni per la scrittura di calcoli e per la memorizzazione di molte formule trigonometriche. La cotangente, la secante e la cosecante non hanno alcun significato specifico. Mentre le figure seguenti possono rappresentare queste funzioni con le lunghezze di segmenti di linea, sarebbe un errore considerare i significati della cotangente, della secante e della cosecante sulla circonferenza trigonometrica. Nelle figure seguenti, solo il seno e il coseno hanno significati visuali.
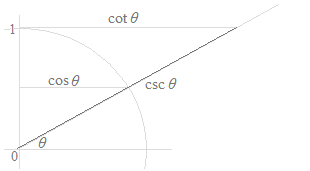
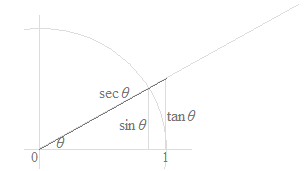
Come curve, soltanto le curve della funzione seno e la funzione coseno sono utilizzate, e le curve della funzione tangente, la funzione cotangente, la funzione secante e la funzione cosecante sono inutili.
Tangente
La tangente è la pendenza m di una curva nel sistema cartesiano, e non è l’angolo θ della circonferenza trigonometrica. La tangente e la circonferenza trigonometrica non hanno relazione diretta.
P( cosθ , sinθ )
Il punto P sembra un punto, ma in realtà, è un cerchio. Il punto P è la circonferenza trigonometrica, e non è una funzione.
Mentre il punto P è un movimento circolare a velocità costante, il seno è il valore di un movimento verticale con una accelerazione che varia.
La relazione reciproca tra la curva della funzione seno e la curva della funzione coseno sarà utilizzata nel calcolo.
y = sin x
y = cos x
