Cercle trigonométrique


“Hier, j’ai composé une chanson.”
“C’est comment, la mélodie?”
“Par exemple, le cinquième croche de la troisième mesure est un mi bémol.”
Les fonctions trigonométriques et le cercle trigonométrique.
La courbe de la fonction sinus est une belle courbe, qui a la pente de 45 degrés, la longueur de π, et l’aire de 2. L’admiration pour la beauté de cette courbe pourrait être la base de la compréhension des fonctions trigonométriques. D’une part, la forme de la courbe de la fonction sinus est très utile pour le calcul différentiel et intégral, d’autre part, le cercle trigonométrique n’est qu’une figure qui montre visuellement la définition de la fonction sinus, et il est autrement inutile.
Le cercle trigonométrique n’est pas la fonction sinus. Le cercle trigonométrique fait des illusions telles que le cercle trigonométrique montre les fonctions trigonométriques, que la fonction sinus et la fonction cosinus sont le mouvement circulaire d’un point P sur le cercle, et que la considération la fonction sinus et de la fonction cosinus sont géométriquement considérées dans le deuxième, le troisième et le quatrième quadrant. Une fois la courbe de la fonction sinus a été faite, le calcul n’a plus besoin du cercle trigonométrique.
Bien qu’il y ait six fonctions trigonométriques, la cotangente, la sécante et la cosécante sont des simplifications du sinus ou du cosinus, qui sont sous forme de fraction. Ce sont des simplifications pour l’écriture de calcul et pour la mémorisation de nombreuses formules trigonométriques. La cotangente, la sécante et la cosécante n’ont pas de signification spécifique. Tandis que les figures ci-dessous peuvent représenter ces fonctions avec des longueurs des segments de droite, ce serait une erreur de considérer les significations de la cotangente, de la sécante et de la cosécante sur le cercle trigonométrique. Dans les figures ci-dessous, seuls le sinus et le cosinus ont des significations visuelles.
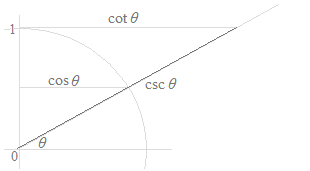
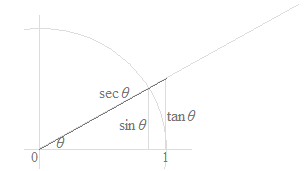
Come les courbes, seules les courbes de la fonction sinus et la fonction cosinus sont utilisées, et les courbes de la fonction tangente, la fonction cotangente, la fonction sécante et la fonction cosécante sont inutiles.
Tangent
La tangent est la pente m de la courbe dans le système cartésien, et ce n’est pas l’angle θ du cercle trigonométrique. La tangente et le cercle trigonométrique n’ont pas de relation directe.
P( cosθ , sinθ )
Le point P ressemble à un point, mais, en fait, c’est un cercle. Le point P est le cercle trigonométrique, et il n’est pas une fonction.
Lorsque le point P est un mouvement circulaire à une vitesse constante, le sinus est la valeur d’un mouvement de monter et descendre avec une accélération changeante.
La relation réciproque entre la courbe de la fonction sinus et la courbe de la fonction cosinus sera utilisée dans le calcul.
y = sin x
y = cos x
