単位円


「きのう、僕は歌を作曲したんだ」
「どんなメロディーですか」
「たとえば、三小節目の五つ目の八分音符はミのフラットなのだ」
三角関数と単位円
サイン関数の曲線は、45度の傾き、π の長さ、そして 2 の面積をもつ美しい曲線です。この曲線の美しさへの畏敬の念こそが三角関数の理解の基本ではないでしょうか。サイン関数の曲線は微積分の計算のためにとても便利な形をしています。それに対し、単位円はサイン関数の定義を視覚的に示す単なる図であり、何の役にも立ちません。
単位円は三角関数を表してはいません。単位円が三角関数であるかような錯覚、サイン関数とコサイン関数が単位円上の点 P の円運動であるかような錯覚、第二象限、第三象限、第四象限でサインとコサインを幾何学的に考えようとする錯覚には注意が必要です。サイン関数の曲線ができあがったら、もう単位円には用はありません。
サインとコサイン
三角関数には六つありますが、コタンジェント、セカント、コセカントは分数の形におけるサインとコサインの簡素化にすぎません。計算を書くときの簡素化、および公式の暗記の際の簡素化です。コタンジェント、セカント、コセカントは、各々の固有の意味はもっていません。第一象限では線分の長さとして下の図のように表すことはできるのですが、コタンジェント、セカント、コセカントの単位円での意味を考えるのは誤りです。下の図では、サインとコサイン以外は視覚的な意味をもちません。
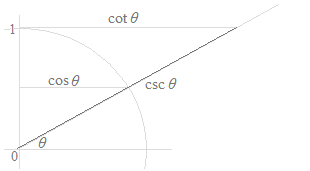
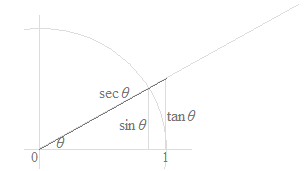
また、グラフはサイン関数のグラフとコサイン関数のグラフのみが使われるであり、タンジェント関数、コタンジェント関数、セカント関数、コセカント関数のグラフは何の役にも立ちません。
タンジェント
タンジェントはグラフの傾き m であり、単位円の θ ではありません。タンジェントと単位円は直接的な関係はありません。
点 P(cosθ , sinθ)
点 P は、ひとつの点のように見えますが、じつは円です。点 P は単位円であり、関数ではありません。点 P は等速の円運動ですが、サインは変化する加速度とともに上下運動をする値です。
微積分の計算では、サイン関数の曲線とコサイン関数の曲線の相互関係が使われます。
y = sin x
y = cos x
