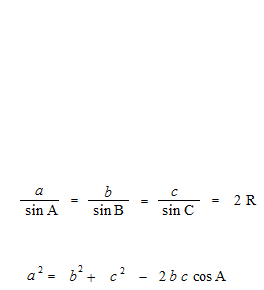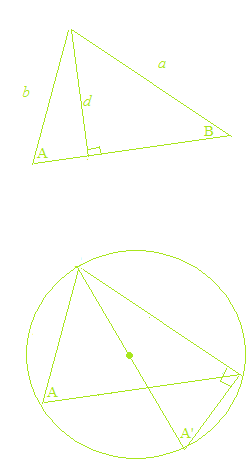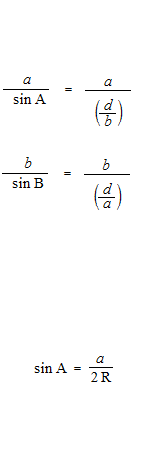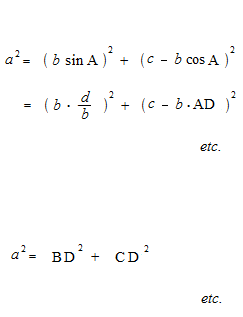Razões trigonométricas de um ângulo obtuso, lei dos senos, lei dos cossenos
O seno de um ângulo obtuso e o cosseno de um ângulo obtuso
As razões trigonométricas
O seno, o cosseno e a tangente são razões entre os comprimentos dos lados de um triângulo rectângulo. Estes são razões entre os comprimentos, que são valores absolutos, de dois lados. O seno, o cosseno e a tangente foram definidos só para os lados de um triângulo rectângulo.¤ Não há seno de um ângulo obtuso, cosseno de um ângulo obtuso, tangente de um ângulo obtuso.
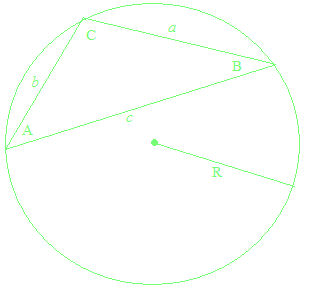
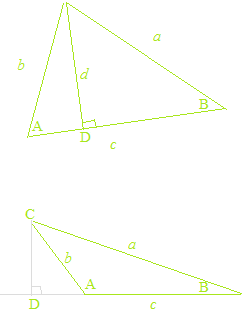
A lei dos senos com um ângulo obtuso e a lei dos cossenos com um ângulo obtuso
Tomando, para o seno de um ângulo obtuso, o valor do seno do seu ângulo suplementar, e para o coseno de um ângulo obtuso, o valor do cosseno do seu ângulo suplementar, a lei dos senos e a lei dos cossenos são válidas mesmo para os triângulos obtusos.
A lei dos senos e a lei dos cossenos são teoremas puramente geométricos e não têm nada a ver com as funções trigonométricas. Também, nas provas da lei dos senos e da lei dos cossenos, o valor do seno do ângulo suplementar é utilizado para o seno de um ângulo obtuso, e o valor do coseno do ângulo suplementar é usado para o coseno de um ângulo obtuso. Como a geometria, o cálculo é sempre com valores absolutos. Pela confusão das funções trigonométricas e as razões trigonométricas, explicações da lei dos senos e da lei dos cossenos com as funções trigonométricas e a circunferência trigonométrica são obviamente erros. Às vezes, há explicações errôneas, como “o seno de um ângulo obtuso e o seno de um ângulo agudo têm o mesmo valor”, etc.
Função
Em geral, as funções são operações com uma variável independente que determinam um único valor da variável dependente, e funções podem ser livremente criadas com definições livremente escolhidas. Por exemplo, uma função pode ser criada com uma variável independente para as datas e uma variável dependente para a temperatura ao meio-dia em Nova Delhi.
O seno de um ângulo obtuso e o coseno de um ângulo obtuso
As razões trigonométricas não podem ser utilizados para um ângulo obtuso. Era uma vez, um matemático que inventou duas funções. Elas foram definidas como as razões trigonométricas no primeiro quadrante da circunferência trigonométrica, em seguida, com a simetria vertical e horizontal. Elas representavam valores de comprimento positivos ou negativos, e não proporção de valores absolutos. A circunferência trigonométrica foi uma maneira de mostrar as definições. O matemático chamou essas duas funções artificialmente definidas “a função seno” e “a função cosseno”. As razões trigonométricas nunca podem ser utilizadas para as ângulos obtusos. Este senhor tem fabricados duas funções que têm a rotação como definição, e nomeou-as “a função seno” e “a função cosseno”.
A lei dos senos e a lei dos cossenos