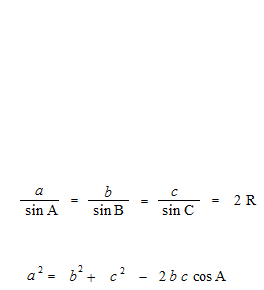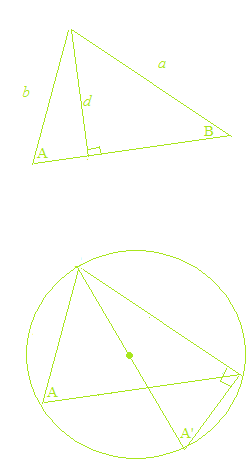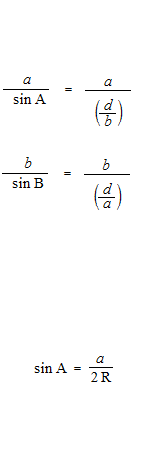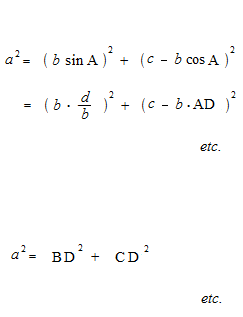Trigonometrische Verhältnisse eines Stumpfen Winkels, Sinussatz, Kosinussatz
Sinus eines Stumpfen Winkels und Kosinus eines Stumpfen Winkels
Die trigonometrische Verhältnisse
Sinus, Kosinus und Tangens sind Verhältnisse zwischen den Seitenlängen im rechtwinkligen Dreieck. Dies sind Verhältnisse zwischen den Längen von zwei Seiten, die Absolutwerte sind. Sinus, Kosinus und Tangens sind nur für die Seitenlängen in einem rechtwinkligen Dreiecke definiert worden. ¤Es gibt keinen Sinus eines stumpfen Winkels, keinen Kosinus eines stumpfen Winkels, keinen Tangens eines stumpfen Winkels.
Der Sinussatz mit einem stumpfen Winkel und der Kosinussatz mit einem stumpfen Winkel
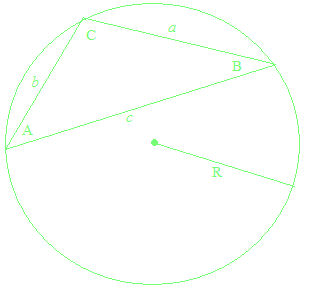
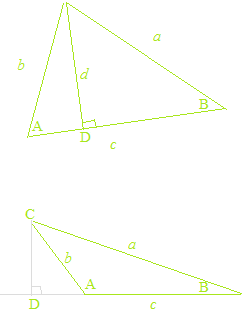
Man nimmt, für Sinus eines stumpfen Winkels, den Wert des Sinus des Supplementwinkels, und für Kosinus eines stumpfen Winkels, den Wert des Kosinus des Supplementwinkels, sind der Sinussatz und der Kosinussatz sogar für stumpfe Dreiecke gültig.
Der Sinussatz und der Kosinussatz sind rein geometrische Theoreme und haben nichts mit den trigonometrischen Funktionen zu tun. Auch in den Beweisen des Sinussatzes und des Kosinussatzes, werden der Wert des Sinus des Supplementwinkels für Sinus eines stumpfen Winkels, und der Wert des Kosinus des Supplementwinkels für Kosinus eines stumpfen Winkels verwendet. Als die Geometrie, ist die Berechnung immer mit absoluten Werten. Durch die Verwirrung der trigonometrischen Funktionen und der trigonometrischen Verhältnisse, sind Erklärungen des Sinussatzes und des Kosinussatzes mit den trigonometrischen Funktionen und dem Einheitskreis offensichtlich Fehler. Manchmal gibt es fehlerhafte Erklärungen, wie “Sinus eines stumpfen Winkels und Sinus eines spitzen Winkels haben den gleichen Wert”, usw.
Funktion
Im allgemeinen sind die Funktionen, Operationen mit einer unabhängigen Variable, die nur einen Wert der abhängigen Variable bestimmen, und Funktionen können mit frei gewählten Definitionen frei gemacht werden. Zum Beispiel kann eine Funktion mit einer unabhängigen Variable für die Daten und einer abhängigen Variable für die Temperatur am Mittag in Neu-Delhi gemacht werden.
Sinus eines stumpfen Winkels und Cosinus eines stumpfen Winkels
Die trigonometrischen Verhältnisse können nicht für einen stumpfen Winkel verwendet werden. Es war einmal, ein Mathematiker, der zwei Funktionen erfand. Diese Funktionen wurden als die trigonometrische Verhältnisse in dem ersten Quadranten des Einheitskreises definiert, dann, mit der vertikalen und horizontalen Symmetrie. Sie repräsentierten positiven oder negativen Längenwerte, und nicht Verhältnisse von absoluten Werten. Der Einheitskreis war eine Art, Definitionen zu zeigen. Der Mathematiker hat diese zwei Funktionen, die künstlich definiert wurden, “Sinus-Funktion” und “Cosinus-Funktion” genannt. Die trigonometrische Verhältnisse können nie für stumpfe Winkel verwendet werden. Dieser Mann hat zwei Funktionen gemacht hat, die die Rotation als Definition hat, und “die Sinusfunktion” und “Cosinusfunktion” genannt.
Sinussatz und Kosinussatz