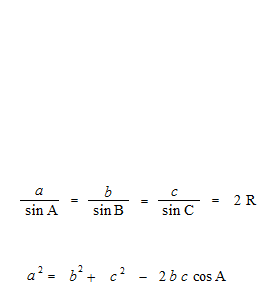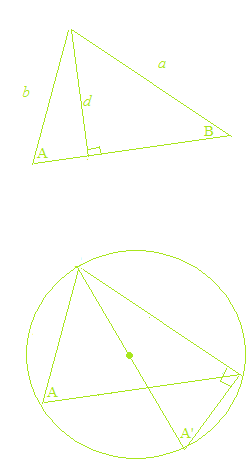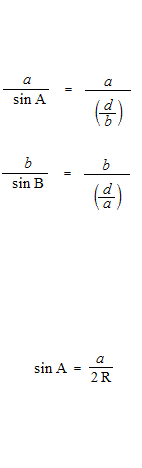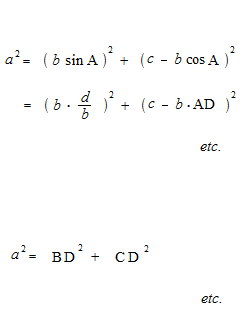Trigonometric ratios of an obtuse angle, Law of sines, Law of cosines
Sine of an obtuse angle, cosine of an obtuse angle
The primary trigonometric ratios
Sine, cosine and tangent are ratios between the lengths of the sides of a right triangle. These are ratios between the lengths of two sides, which are absolute values. Sine, cosine and tangent have been defined only for the sides of a right triangle. ¤There is no sine of an obtuse angle, no cosine of an obtuse angle, no tangent of an obtuse angle.
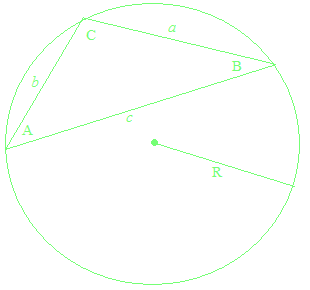
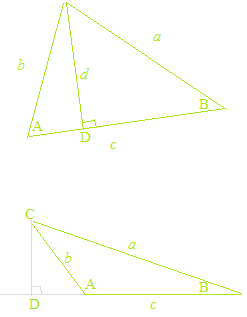
The law of sines with an obtuse angle and the law of cosines with an obtuse angle
As taking, for sine of an obtuse angle, the value of sine of its supplementary angle, and for cosine of an obtuse angle, the value of cosine of its supplementary angle, the law of sines and the law of cosines are valid even for obtuse triangles.
The law of sines and the law of cosines are purely geometric theorems and have nothing to do with the trigonometric functions. Also, in the proofs of the law of sines and the law of cosines, the value of sine of the supplementary angle is used for sine of an obtuse angle, and the value of cosine of the supplementary angle is used for cosine an obtuse angle. As geometry, the calculation is always with absolute values. By the confusion of the trigonometric functions and the trigonometric ratios, explanations of the law of sines and the law of cosines with the trigonometric functions and the unit circle are obviously mistakes. Sometimes there are erroneous explanations, such as “sine of an obtuse angle and sine of an acute angle have the same value,” etc.
Function
In general, the functions are operations with an independent variable, which determine only one value of the dependent variable, and functions can be freely created with freely chosen definitions. For example, a function can be created with an independent variable for the dates and a dependent variable for the temperature at noon in New Delhi.
Sine of an obtuse angle and cosine of an obtuse angle
The trigonometric ratios cannot be used for an obtuse angle. Once upon a time, there was a mathematician who invented two functions. They were defined as the trigonometric ratios in the first quadrant of the unit circle, then, with the vertical and horizontal symmetry. They represented positive or negative length values, and not ratios of absolute values. The unit circle was a way to show the definitions. The mathematician named these two functions, which have been artificially defined, “the sine function” and “the cosine function”. The trigonometric ratios can never be used for obtuse angles. This man fabricated two functions that have rotation as their definition, and named them “the sine function” and “the cosine function”.
The law of sines and the law of cosines