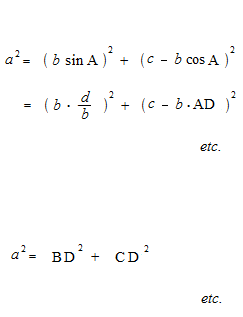鈍角のサイン、鈍角のコサイン、正弦定理と余弦定理
三角比
サイン、コサイン、タンジェントは直角三角形の辺の長さの比率です。二辺の長さの比率、二つの絶対値の比率です。サイン、コサイン、タンジェントは直角三角形のみについて定義されています。鈍角三角形のサイン、鈍角三角形のコサイン、鈍角三角形のタンジェントなどというものはありません。
鈍角の正弦定理と鈍角の余弦定理
鈍角のサインはその補角のサインの比率、鈍角のコサインにはその補角の比率を取るようにするならば、正弦定理と余弦定理は鈍角にも使うことができます。
正弦定理と余弦定理は純粋な幾何学の定理ですから、三角関数とは無関係です。正弦定理と余弦定理の証明においても、鈍角のサインにはその補角のサインが使われ、鈍角のコサインにはその補角のコサインが使われます。幾何学として、常に絶対値で計算されます。三角比と三角関数を混同し、正弦定理と余弦定理の説明に単位円と三角関数を用いるは明らかに間違いです。「鈍角のサインは鋭角のサインと同じだから」などというような説明は間違いです。
関数とは何か。
一般に「関数」とは、ひとつの独立変数が従属変数の値をひとつだけ決定するような関係の表現であり、自由な定義により自由に関数を作ることができます。たとえば、独立変数xを日付、従属変数yをニューデリーの正午の気温と定義しても、それはひとつの関数となります。
鈍角のサイン、鈍角のコサイン
三角比を鈍角に使うことはできません。
昔、ある数学者がふたつの関数を作りました。それらは単位円の第一象限の中の三角比のように定義され、さらに単位円の上下左右の対称性を加えて定義されたものでした。これらの関数に使われる数値は線分の長さにプラスマイナスが付いたものであり、絶対値での比率ではありません。単位円は定義の説明方法にすぎません。彼はこの人為的に定義された関数にサイン関数およびコサイン関数という名前をつけました。三角比が鈍角にも使えるということではありません。彼が、グルグル回転するような定義の関数を作って、それにサイン関数という名前、コサイン関数という名前を付けたのです。彼がサイン関数とコサイン関数の人為的な定義を作った理由は、それらのグラフの曲線の式が数学的に役立つということです。サイン関数とコサイン関数はグラフの曲線の形であり、曲線の式です。たとえば、交流電流の電圧の計算などに使われます。サイン関数とコサイン関数は単位円における事実ではありません。彼は、曲線の式を書くために、独立変数の数値にラジアンを使い、従属変数の数値の定義を単位円を使って図式的に表現したにすぎません。プラスマイナスを付けて定義するのならば、第一象限だけでもよかったのです。関数は自由に定義されますから何も証明することはできません。定理は証明に使われます。人為的な関数の中で、第二象限、第三象限、第四象限の鈍角のサインと鈍角のコサインを、補角として、正弦定理や余弦定理で証明することはできます。しかし、純粋な幾何学的事実であるところの正弦定理や余弦定理を人為的なサイン関数やコサイン関数で証明することはできません。関数は事実を量的に測定することはできますが、事実を証明することはできません。
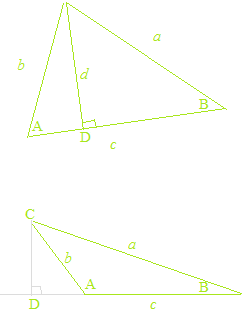
正弦定理と余弦定理
任意の三角形 ABC において
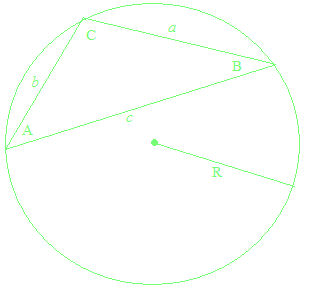
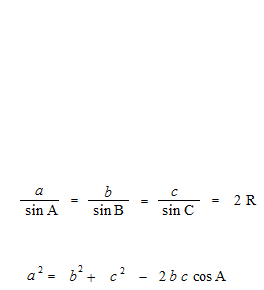
正弦定理の証明
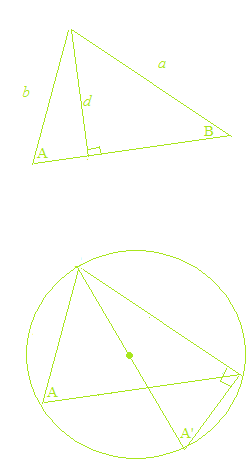
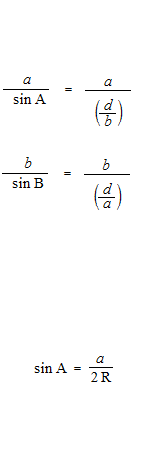
余弦定理の証明