Por qué los argumentos de las funciones trigonométricas son en radianes.
π es un número irracional, 3,14159265359…
“Usar radianes en los cálculos” significa designar el punto 3,14159265359… en el eje horizontal de una gráfica con π, y expresar todos los demás números en ese eje en términos de π.
“Usar radianes en los cálculos” significa “usar π en el eje horizontal de una gráfica”.
Un ángulo, un valor geométrico bidimensional independiente del tamaño de la figura dibujada, se expresa como un valor unidimensional: “la razón entre el arco y el radio”, es decir, “la longitud del arco cuando el radio es igual a 1”.
El argumento es el valor para la variable independiente de una función. Es el valor que será puesto en la variable x de una función f(x)
Sin cálculo diferencial e integral, las funciones trigonométricas no estarían en uso. Mientras que hay a menudo gráficas de las funciones trigonométricas usando coordenadas donde la anchura de la escala del eje horizontal y la anchura de la escala del eje vertical son diferentes, es necesario evitar estas escalas de ejes, como la pendiente y la área son esenciales en el cálculo diferencial e integral.
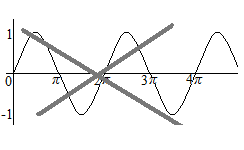

Las coordenadas de gráficos del cálculo diferencial e integral deben tener el mismo ancho de la escala para el eje horizontal y el eje vertical. Hay solamente una “forma” de la curva de la función seno; la altura es entre 1 y −1, y la longitud del ciclo es de 6,28…, respetando la misma escala. Curvas que son horizontalmente cortas no tienen la forma de la curva de la función seno, incluso si sus intersecciones son marcadas con π. Es una idea muy básica del cálculo diferencial e integral.
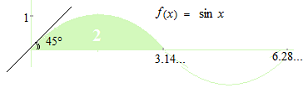
El uso de radianes para las funciones trigonométricas significa que el período de la curva de la función seno es de 6,28… en comparación con 1 en el eje vertical. Como una representación gráfica de la electricidad por un generador eléctrico con la rotación de un conductor en líneas del campo magnético, el eje vertical es la tensión y el eje horizontal es el segundo, por lo tanto, la sinusoide de 1 volt con la frecuencia de 0,159… Hz es la sola curva de la función seno en el cálculo.
La área bajo 1/2 curva de la función seno es de 2 .
Cuando x = 0, la pendiente de la curva de la función seno es de 45 grados, es decir, 1.
La pendiente de la curva de la función seno a x1 es igual al valor de cos x1
La relación entre y = − cos x + c y y = sin x
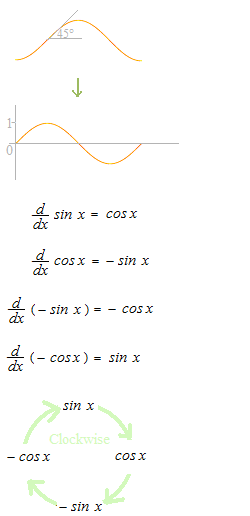

Como una descripción clara de la definición de la función seno, en el círculo unidad, con el ángulo θ como la variable independiente, la variable dependiente se puede representar por el valor que se mueve hacia arriba y hacia abajo en el eje vertical.
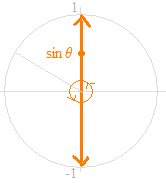
La posición en el movimiento; sin θ
La velocidad del movimiento; cos θ
La aceleración del movimiento; − sin θ
La curva de la función seno con el período de 6,28 … es una herramienta fundamental del cálculo diferencial.
