Why the arguments of the trigonometric functions are in radians.
Argument is the value for the independent variable of a function.
It is the value that will be put in the variable x of a function f(x) .
Without differential and integral calculus, the trigonometric functions would not be in use. While there are often graphs of the trigonometric functions using coordinates where the width of scale of the horizontal axis and the width of scale of the vertical axis are different, it is necessary to avoid these scales of axes, as slope and area are essential in the differential and integral calculus.
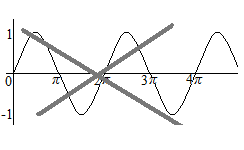

The coordinates for graphs of the differential and integral calculus must have the same width of scale for the horizontal axis and the vertical axis. There is only one “form” of the curve of the sine function; the height is between 1 and −1, and the cycle length is 6.28 …, respecting equal scales. Curves that are horizontally short don’t have the form of the curve of the sine function, even if their intersections are marked with π. This is a very basic idea of the differential and integral calculus.
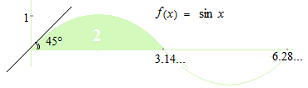
Using radians for trigonometric functions means that the period of the curve of the sine function is 6.28… compared to 1 on the vertical axis. As in a graphical display of electricity of an electric generator by the rotation of a conductor in magnetic field lines, the vertical axis is voltage and the horizontal axis is second, the curve of 1 volt with frequency 0.159… Hz is the only one form of the sine function in the calculus.
The area under 1/2 curve of the sine function is 2.
When x = 0, the slope of the curve of the sine function is 45 degrees, that is, 1.
The slope of the curve of the sine function at x1 is equal to the value of cos x1
The relationship between y = − cos x+ c and y = sin x
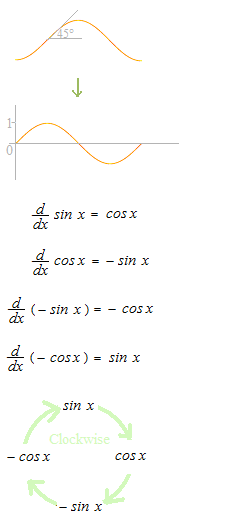

As a clear description of the definition of the sine function, on the unit circle, with the angle θ as the independent variable, the dependent variable can be represented by the value that moves upward and downward on the vertical axis.
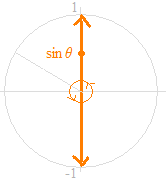
The position in the movement; sin θ
The speed of the movement; cos θ
The acceleration of the movement; − sin θ
The curve of the sine function with period 6.28 … is a principal tool of calculus.
