Pourquoi les arguments des fonctions trigonométriques sont en radians.
Pi est un nombre irrationnel, 3,14159265359…
« Utiliser les radians dans les calculs » signifie désigner le point 3,14159265359… sur l’axe horizontal d’un graphique par π, et exprimer tous les autres nombres sur cet axe avec π.
« Utiliser les radians dans les calculs » signifie « utiliser π sur l’axe horizontal d’un graphique ».
Un angle, valeur géométrique bidimensionnelle, indépendant de la taille de la figure dessinée, est exprimé comme une valeur unidimensionnelle : « le rapport de l’arc au rayon », autrement dit, « la longueur de l’arc lorsque le rayon est égal à 1 ».
Argument, c’est la valeur pour la variable indépendante d’une fonction.
La valeur qui sera mise dans la variable x d’une fonction f(x) .
Sans le calcul différentiel et intégral, les fonctions trigonométriques n’auraient pas d’utilité. Tandis qu’il y a souvent des graphiques des fonctions trigonométriques utilisant des coordonnées où la largeur de l’échelle de l’axe horizontal et celle de l’axe vertical sont différentes, il faut éviter ces échelles des axes, car la pente et l’aire sont essentielles dans le calcul différentiel et intégral.
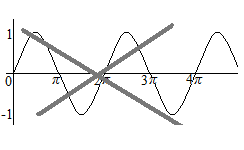

Les coordonnées pour des graphes du calcul différentiel et intégral doivent avoir la même largeur d’échelle pour l’axe horizontal et pour l’axe vertical. Il n’y a qu’une seule “forme” de la courbe de la fonction sinus; la hauteur est entre 1 et −1, et la longueur de cycle est de 6.28…, en respectant les échelles égales. Des courbes qui sont horizontalement courtes n’ont pas la forme de la courbe de la fonction sinus, même si leurs intersections sont marquées avec π. C’est une idée très basique du calcul différentiel et intégral.
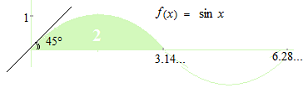
L’utilisation du radian pour les fonctions trigonométriques, cela signifie que la période de la courbe de la fonction sinus est de 6,28… par rapport à 1 sur l’axe vertical. Comme une représentation graphique de l’électricité d’un générateur électrique par la rotation d’un conducteur dans les lignes de champ magnétique, l’axe vertical est le voltage et l’axe horizontal est la seconde, la courbe de 1 volt avec la fréquence 0,159… Hz est la seule forme de la fonction sinus dans le calcul.
L’aire sous 1/2 courbe de la fonction sinus est de 2 .
Quand x = 0 , la pente de la courbe de la fonction sinus est de 45 degrés, c’est-à-dire, 1 .
La pente à x1 de la courbe de la fonction sinus est égal à la valeur de cos x1
La relation entre y = − cos x + c et y = sin x
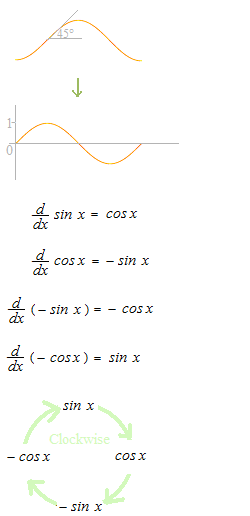

Comme une description claire de la définition de la fonction sinus, sur le cercle unité, avec l’angle θ comme la variable indépendante, la variable dépendante peut être représentée par la valeur qui se déplace vers le haut et vers le bas sur l’axe vertical.
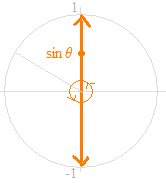
La position dans ce mouvement; sin θ
La vitesse du mouvement; cos θ
L’accélération du mouvement; − sin θ
La courbe de la fonction sinus avec la période 6,28 … est un outil principal du calcul différentiel.
